Esta é a terceira parte de uma série sobre soluções para o desafio do gerador de séries numéricas. Na Parte 1, abordei soluções que geram as linhas em tempo real. Na Parte 2, abordei soluções que consultam uma tabela base física que você preenche previamente com linhas. Este mês, vou me concentrar em uma técnica fascinante que pode ser usada para lidar com nosso desafio, mas que também tem aplicações interessantes muito além disso. Não conheço um nome oficial para a técnica, mas é um pouco semelhante em conceito à eliminação de partição horizontal, então vou me referir a ela informalmente como eliminação de unidade horizontal técnica. A técnica pode ter benefícios de desempenho positivos interessantes, mas também há ressalvas que você precisa estar ciente, onde sob certas condições pode incorrer em uma penalidade de desempenho.
Obrigado novamente a Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea e Paul White por compartilhar suas ideias e comentários.
Farei meus testes no tempdb, habilitando as estatísticas de tempo:
SET NOCOUNT ON; USE tempdb; SET STATISTICS TIME ON;
Ideias anteriores
A técnica de eliminação de unidade horizontal pode ser usada como alternativa à lógica de eliminação de coluna, ou eliminação de unidade vertical técnica, na qual confiei em várias das soluções que abordei anteriormente. Você pode ler sobre os fundamentos da lógica de eliminação de coluna com expressões de tabela em Fundamentos de expressões de tabela, Parte 3 – Tabelas derivadas, considerações de otimização em “Projeção de coluna e uma palavra em SELECT *.”
A ideia básica da técnica de eliminação de unidade vertical é que, se você tiver uma expressão de tabela aninhada que retorne as colunas x e y, e sua consulta externa fizer referência apenas à coluna x, o processo de compilação da consulta eliminará y da árvore de consulta inicial e, portanto, o plano não precisa avaliar. Isso tem várias implicações positivas relacionadas à otimização, como alcançar a cobertura do índice apenas com x e, se y for resultado de uma computação, não será necessário avaliar a expressão subjacente de y. Essa ideia estava no centro da solução de Alan Burstein. Também confiei nele em várias das outras soluções que abordei, como com a função dbo.GetNumsAlanCharlieItzikBatch (da Parte 1), as funções dbo.GetNumsJohn2DaveObbishAlanCharlieItzik e dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 (da Parte 2) e outras. Como exemplo, usarei dbo.GetNumsAlanCharlieItzikBatch como a solução de linha de base com a lógica de eliminação vertical.
Como lembrete, esta solução usa uma junção com uma tabela fictícia que possui um índice columnstore para obter o processamento em lote. Aqui está o código para criar a tabela fictícia:
DROP TABLE IF EXISTS dbo.BatchMe; GO CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
E aqui está o código com a definição da função dbo.GetNumsAlanCharlieItzikBatch:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Usei o seguinte código para testar o desempenho da função com 100M de linhas, retornando a coluna do resultado computado n (manipulação do resultado da função ROW_NUMBER), ordenada por n:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
Aqui estão as estatísticas de tempo que obtive para este teste:
Tempo de CPU =9328 ms, tempo decorrido =9330 ms.
Usei o seguinte código para testar o desempenho da função com 100M de linhas, retornando a coluna rn (direta, não manipulada, resultado da função ROW_NUMBER), ordenada por rn:
DECLARE @n AS BIGINT; SELECT @n = rn FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY rn OPTION(MAXDOP 1);
Aqui estão as estatísticas de tempo que obtive para este teste:
Tempo de CPU =7296 ms, tempo decorrido =7291 ms.
Vamos rever as ideias importantes que estão incorporadas nesta solução.
Baseando-se na lógica de eliminação de colunas, alan teve a ideia de retornar não apenas uma coluna com a série numérica, mas três:
- Coluna rn representa um resultado não manipulado da função ROW_NUMBER, que começa com 1. É barato calcular. É a preservação da ordem quando você fornece constantes e quando você fornece não constantes (variáveis, colunas) como entradas para a função. Isso significa que quando sua consulta externa usa ORDER BY rn, você não recebe um operador Sort no plano.
- Coluna n representa um cálculo baseado em @low, uma constante e rownum (resultado da função ROW_NUMBER). É a preservação da ordem em relação ao rownum quando você fornece constantes como entradas para a função. Isso se deve à visão de Charlie sobre dobras constantes (consulte a Parte 1 para obter detalhes). No entanto, não há preservação de ordem quando você fornece inconstantes como entradas, pois você não obtém dobras constantes. Demonstrarei isso mais adiante na seção sobre advertências.
- Coluna op representa n na ordem oposta. É o resultado de uma computação e não preserva a ordem.
Baseando-se na lógica de eliminação de colunas, se você precisar retornar uma série numérica começando com 1, você consulta a coluna rn, que é mais barata do que consultar n. Se você precisar de uma série numérica começando com um valor diferente de 1, você consulta n e paga o custo extra. Se você precisar do resultado ordenado pela coluna numérica, com constantes como entradas, você pode usar ORDER BY rn ou ORDER BY n. Mas com inconstantes como entradas, você quer certificar-se de usar ORDER BY rn. Pode ser uma boa ideia sempre usar ORDER BY rn quando precisar que o resultado ordenado esteja no lado seguro.
A ideia de eliminação de unidade horizontal é semelhante à ideia de eliminação de unidade vertical, só que se aplica a conjuntos de linhas em vez de conjuntos de colunas. Na verdade, Joe Obbish baseou-se nessa ideia em sua função dbo.GetNumsObbish (da Parte 2), e vamos dar um passo adiante. Em sua solução, Joe unificou várias consultas representando subintervalos disjuntos de números, usando um filtro na cláusula WHERE de cada consulta para definir a aplicabilidade do subintervalo. Quando você chama a função e passa entradas constantes representando os delimitadores do intervalo desejado, o SQL Server elimina as consultas inaplicáveis em tempo de compilação, de modo que o plano nem as reflete.
Eliminação de unidade horizontal, tempo de compilação versus tempo de execução
Talvez seja uma boa ideia começar demonstrando o conceito de eliminação horizontal de unidades em um caso mais geral e também discutir uma importante distinção entre eliminação em tempo de compilação e eliminação em tempo de execução. Então podemos discutir como aplicar a ideia ao nosso desafio da série numérica.
Usarei três tabelas chamadas dbo.T1, dbo.T2 e dbo.T3 no meu exemplo. Use o seguinte código DDL e DML para criar e preencher essas tabelas:
DROP TABLE IF EXISTS dbo.T1, dbo.T2, dbo.T3; GO CREATE TABLE dbo.T1(col1 INT); INSERT INTO dbo.T1(col1) VALUES(1); CREATE TABLE dbo.T2(col1 INT); INSERT INTO dbo.T2(col1) VALUES(2); CREATE TABLE dbo.T3(col1 INT); INSERT INTO dbo.T3(col1) VALUES(3);
Suponha que você queira implementar um TVF embutido chamado dbo.OneTable que aceite um dos três nomes de tabela acima como entrada e retorne os dados da tabela solicitada. Com base no conceito de eliminação de unidade horizontal, você pode implementar a função assim:
CREATE OR ALTER FUNCTION dbo.OneTable(@WhichTable AS NVARCHAR(257)) RETURNS TABLE AS RETURN SELECT col1 FROM dbo.T1 WHERE @WhichTable = N'dbo.T1' UNION ALL SELECT col1 FROM dbo.T2 WHERE @WhichTable = N'dbo.T2' UNION ALL SELECT col1 FROM dbo.T3 WHERE @WhichTable = N'dbo.T3'; GO
Lembre-se de que um TVF embutido aplica a incorporação de parâmetros. Isso significa que quando você passa uma constante como N'dbo.T2' como entrada, o processo de inserção substitui todas as referências a @WhichTable pela constante antes da otimização . O processo de eliminação pode então remover as referências a T1 e T3 da árvore de consulta inicial e, assim, a otimização da consulta resulta em um plano que faz referência apenas a T2. Vamos testar essa ideia com a seguinte consulta:
SELECT * FROM dbo.OneTable(N'dbo.T2');
O plano para esta consulta é mostrado na Figura 1.
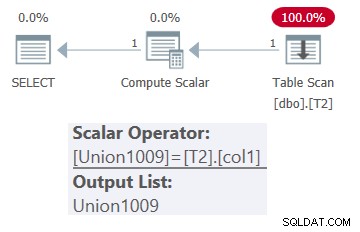Figura 1:plano para dbo.OneTable com entrada constante Como você pode ver, apenas a tabela T2 aparece no plano.
As coisas são um pouco mais complicadas quando você passa uma inconstante como entrada. Este pode ser o caso ao usar uma variável, um parâmetro de procedimento ou passar uma coluna via APPLY. O valor de entrada é desconhecido em tempo de compilação ou o potencial de reutilização do plano parametrizado precisa ser levado em consideração.
O otimizador não pode eliminar nenhuma das tabelas do plano, mas ainda tem um truque. Ele pode usar operadores de filtro de inicialização acima das subárvores que acessam as tabelas e executar apenas a subárvore relevante com base no valor de tempo de execução de @WhichTable. Use o código a seguir para testar essa estratégia:
DECLARE @T AS NVARCHAR(257) = N'dbo.T2'; SELECT * FROM dbo.OneTable(@T);
O plano para esta execução é mostrado na Figura 2:
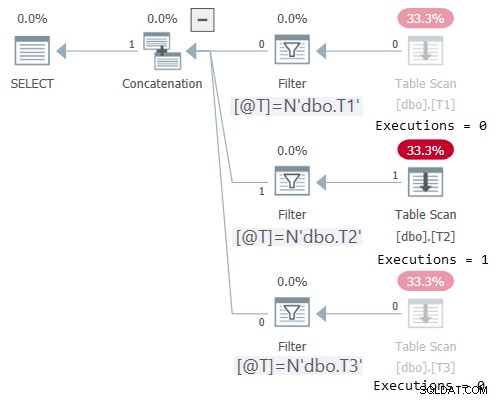Figura 2:plano para dbo.OneTable com entrada não constante O Plan Explorer torna maravilhosamente óbvio ver que apenas a subárvore aplicável foi executada (Executions =1) e desativa as subárvores que não foram executadas (Executions =0). Além disso, STATISTICS IO mostra informações de E/S apenas para a tabela que foi acessada:
Tabela 'T2'. Contagem de varredura 1, leitura lógica 1, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 0, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Aplicando a lógica de eliminação de unidade horizontal ao desafio da série numérica
Conforme mencionado, você pode aplicar o conceito de eliminação de unidade horizontal modificando qualquer uma das soluções anteriores que atualmente usam a lógica de eliminação vertical. Usarei a função dbo.GetNumsAlanCharlieItzikBatch como ponto de partida para o meu exemplo.
Lembre-se de que Joe Obbish usou a eliminação horizontal de unidades para extrair os subintervalos disjuntos relevantes da série numérica. Usaremos o conceito para separar horizontalmente a computação mais barata (rn) onde @low =1 da computação mais cara (n) onde @low <> 1.
Enquanto estamos nisso, podemos experimentar adicionando a ideia de Jeff Moden em sua função fnTally, onde ele usa uma linha sentinela com o valor 0 para casos em que o intervalo começa com @low =0.
Então temos quatro unidades horizontais:
- Linha sentinela com 0 em que @low =0, com n =0
- Linhas TOP (@high) em que @low =0, com barato n =rownum e op =@high – rownum
- Linhas TOP (@high) em que @low =1, com barato n =rownum e op =@high + 1 – rownum
- TOP(@high – @low + 1) linhas onde @low <> 0 AND @low <> 1, com mais caro n =@low – 1 + rownum e op =@high + 1 – rownum
Esta solução combina ides de Alan, Charlie, Joe, Jeff e eu, então chamaremos a versão em modo de lote da função dbo.GetNumsAlanCharlieJoeJeffItzikBatch.
Primeiro, lembre-se de certificar-se de que você ainda tem a tabela fictícia dbo.BatchMe presente para obter o processamento em lote em nossa solução ou use o seguinte código se não tiver:
DROP TABLE IF EXISTS dbo.BatchMe; GO CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Aqui está o código com a definição da função dbo.GetNumsAlanCharlieJoeJeffItzikBatch:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeJeffItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT @low AS n, @high AS op WHERE @low = 0 AND @high > @low
UNION ALL
SELECT TOP(@high)
rownum AS n,
@high - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 0
ORDER BY rownum
UNION ALL
SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 1
ORDER BY rownum
UNION ALL
SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low <> 0 AND @low <> 1
ORDER BY rownum;
GO Importante:O conceito de eliminação de unidade horizontal é sem dúvida mais complexo de implementar do que o vertical, então por que se preocupar? Porque retira do usuário a responsabilidade de escolher a coluna certa. O usuário só precisa se preocupar em consultar uma coluna chamada n, em vez de se lembrar de usar rn quando o intervalo começar com 1 e n caso contrário.
Vamos começar testando a solução com as entradas constantes 1 e 100.000.000, pedindo que o resultado seja ordenado:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 3.
Figura 3:Plano para dbo.GetNumsAlanCharlieJoeJeffItzikBatch(1, 100M) Observe que a única coluna retornada é baseada na expressão ROW_NUMBER direta e não manipulada (Expr1313). Observe também que não há necessidade de classificação no plano.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =7359 ms, tempo decorrido =7354 ms.
O tempo de execução reflete adequadamente o fato de que o plano usa o modo de lote, a expressão ROW_NUMBER não manipulada e nenhuma classificação.
Em seguida, teste a função com o intervalo constante de 0 a 99.999.999:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(0, 99999999) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 4.
Figura 4:Plano para dbo.GetNumsAlanCharlieJoeJeffItzikBatch(0, 99999999) O plano usa um operador Merge Join (Concatenação) para mesclar a linha sentinela com o valor 0 e o restante. Mesmo que a segunda parte seja tão eficiente quanto antes, a lógica de mesclagem cobra um preço bastante alto de cerca de 26% no tempo de execução, resultando nas seguintes estatísticas de tempo:
Tempo de CPU =9265 ms, tempo decorrido =9298 ms.
Vamos testar a função com o intervalo constante de 2 a 100.000.001:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(2, 100000001) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 5.
Figura 5:Plano para dbo.GetNumsAlanCharlieJoeJeffItzikBatch(2, 100000001) Desta vez, não há lógica de mesclagem cara, pois a parte da linha sentinela é irrelevante. No entanto, observe que a coluna retornada é a expressão manipulada @low – 1 + rownum, que após o parâmetro embedding/inlining e constante folding tornou-se 1 + rownum.
Aqui estão as estatísticas de tempo que obtive para esta execução:
Tempo de CPU =9000 ms, tempo decorrido =9015 ms.
Como esperado, isso não é tão rápido quanto com um intervalo que começa com 1, mas curiosamente, mais rápido do que com um intervalo que começa com 0.
Removendo a linha sentinela 0
Dado que a técnica com a linha sentinela com o valor 0 parece ser mais lenta do que aplicar manipulação a rownum, faz sentido simplesmente evitá-la. Isso nos leva a uma solução simplificada baseada em eliminação horizontal que mistura as ideias de Alan, Charlie, Joe e eu. Vou chamar a função com esta solução dbo.GetNumsAlanCharlieJoeItzikBatch. Aqui está a definição da função:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 1
ORDER BY rownum
UNION ALL
SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low <> 1
ORDER BY rownum;
GO Vamos testá-lo com o intervalo de 1 a 100M:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
O plano é o mesmo mostrado anteriormente na Figura 3, como esperado.
Assim, obtive as seguintes estatísticas de tempo:
Tempo de CPU =7219 ms, tempo decorrido =7243 ms.
Teste-o com o intervalo de 0 a 99.999.999:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(0, 99999999) ORDER BY n OPTION(MAXDOP 1);
Desta vez, você obtém o mesmo plano mostrado anteriormente na Figura 5 - não na Figura 4.
Aqui estão as estatísticas de tempo que obtive para esta execução:
Tempo de CPU =9313 ms, tempo decorrido =9334 ms.
Teste-o com o intervalo de 2 a 100.000.001:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(2, 100000001) ORDER BY n OPTION(MAXDOP 1);
Novamente, você obtém o mesmo plano mostrado anteriormente na Figura 5.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =9125 ms, tempo decorrido =9148 ms.
Avisos ao usar entradas não constantes
Com as técnicas de eliminação de unidade vertical e horizontal, as coisas funcionam de maneira ideal desde que você passe constantes como entradas. No entanto, você precisa estar ciente das ressalvas que podem resultar em penalidades de desempenho ao passar entradas não constantes. A técnica de eliminação de unidade vertical tem menos problemas, e os problemas que existem são mais fáceis de lidar, então vamos começar com ela.
Lembre-se que neste artigo usamos a função dbo.GetNumsAlanCharlieItzikBatch como nosso exemplo que se baseia no conceito de eliminação de unidade vertical. Vamos executar uma série de testes com entradas não constantes, como variáveis.
Como nosso primeiro teste, retornaremos rn e solicitaremos os dados ordenados por rn:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000; DECLARE @n AS BIGINT; SELECT @n = rn FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY rn OPTION(MAXDOP 1);
Lembre-se de que rn representa a expressão ROW_NUMBER não manipulada, portanto, o fato de usarmos entradas não constantes não tem significado especial neste caso. Não há necessidade de classificação explícita no plano.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =7390 ms, tempo decorrido =7386 ms.
Esses números representam o caso ideal.
No próximo teste, ordene as linhas de resultado por n:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000; DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 6.
Figura 6:Plano para dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ordenação por n Veja o problema? Após o inlining, @low foi substituído por @mylow—não pelo valor em @mylow, que é 1. Consequentemente, a dobragem constante não ocorreu e, portanto, n não preserva a ordem em relação ao rownum. Isso resultou em classificação explícita no plano.
Aqui estão as estatísticas de tempo que obtive para esta execução:
Tempo de CPU =25141 ms, tempo decorrido =25628 ms.
O tempo de execução quase triplicou em comparação com quando a classificação explícita não era necessária.
Uma solução simples é usar a ideia original de Alan Burstein de sempre ordenar por rn quando você precisar do resultado ordenado, tanto ao retornar rn quanto ao retornar n, assim:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000; DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY rn OPTION(MAXDOP 1);
Desta vez, não há classificação explícita no plano.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =9156 ms, tempo decorrido =9184 ms.
Os números refletem adequadamente o fato de que você está retornando a expressão manipulada, mas não incorrendo em nenhuma classificação explícita.
Com soluções baseadas na técnica de eliminação de unidade horizontal, como nossa função dbo.GetNumsAlanCharlieJoeItzikBatch, a situação é mais complicada ao usar entradas não constantes.
Vamos primeiro testar a função com um intervalo muito pequeno de 10 números:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 10; DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 7.
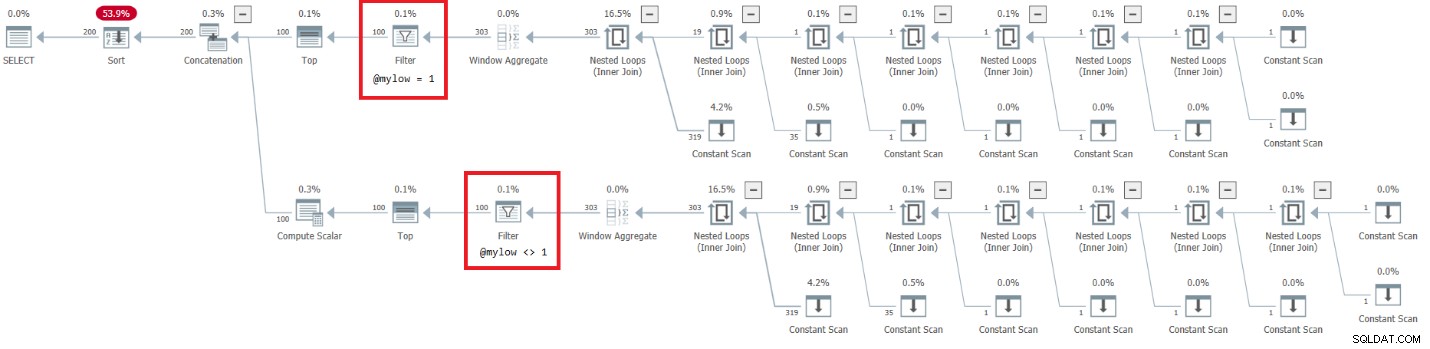Figura 7:Plano para dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) Há um lado muito alarmante nesse plano. Observe que os operadores de filtro aparecem abaixo os principais operadores! Em qualquer chamada à função com entradas não constantes, naturalmente uma das ramificações abaixo do operador Concatenação sempre terá uma condição de filtro falsa. No entanto, ambos os operadores Top solicitam um número diferente de zero de linhas. Portanto, o operador Top acima do operador com a condição de filtro falso solicitará linhas e nunca será satisfeito, pois o operador de filtro continuará descartando todas as linhas que obterá de seu nó filho. O trabalho na subárvore abaixo do operador Filtro terá que ser executado até a conclusão. No nosso caso isso significa que a subárvore passará pelo trabalho de gerar 4B linhas, que o operador Filter irá descartar. Você se pergunta por que o operador de filtro se incomoda em solicitar linhas de seu nó filho, mas parece que é assim que funciona atualmente. É difícil ver isso com um plano estático. É mais fácil ver isso ao vivo, por exemplo, com a opção de execução de consulta ao vivo no SentryOne Plan Explorer, conforme mostrado na Figura 8. Experimente.
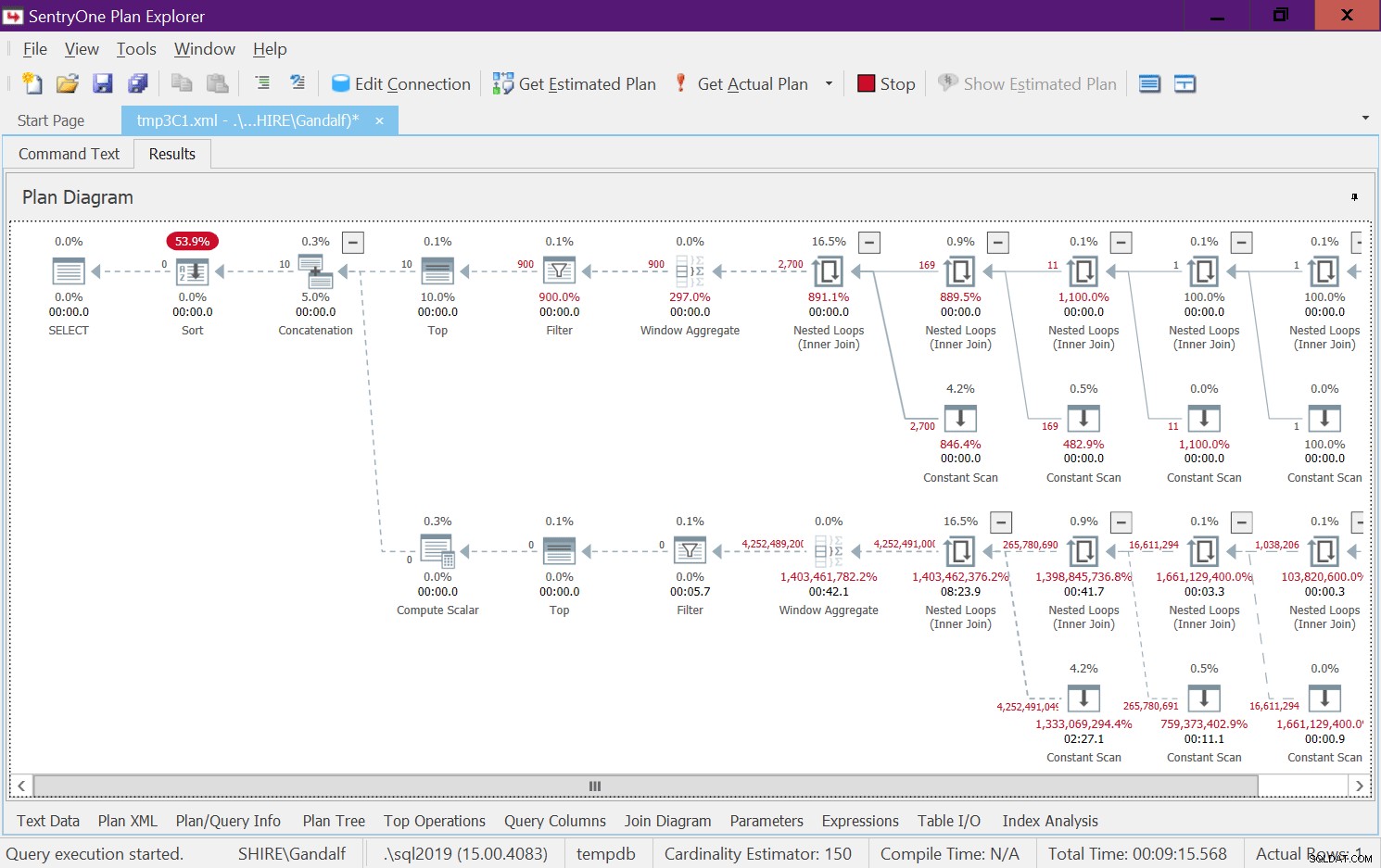Figura 8:Estatísticas de consulta ao vivo para dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) Este teste demorou 9:15 minutos para ser concluído na minha máquina, e lembre-se que o pedido era para retornar um intervalo de 10 números.
Vamos pensar se há uma maneira de evitar a ativação da subárvore irrelevante em sua totalidade. Para conseguir isso, você deseja que os operadores de filtro de inicialização apareçam acima os operadores Top em vez de abaixo deles. Se você ler Fundamentos de expressões de tabela, Parte 4 – Tabelas derivadas, considerações de otimização, continuação, saberá que um filtro TOP impede o desaninhamento de expressões de tabela. Portanto, tudo o que você precisa fazer é colocar a consulta TOP em uma tabela derivada e aplicar o filtro em uma consulta externa na tabela derivada.
Aqui está nossa função modificada implementando este truque:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT *
FROM ( SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum ) AS D1
WHERE @low = 1
UNION ALL
SELECT *
FROM ( SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum ) AS D2
WHERE @low <> 1;
GO Como esperado, as execuções com constantes continuam se comportando e realizando o mesmo que sem o truque.
Quanto às entradas não constantes, agora com intervalos pequenos é muito rápido. Aqui está um teste com um intervalo de 10 números:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 10; DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 9.
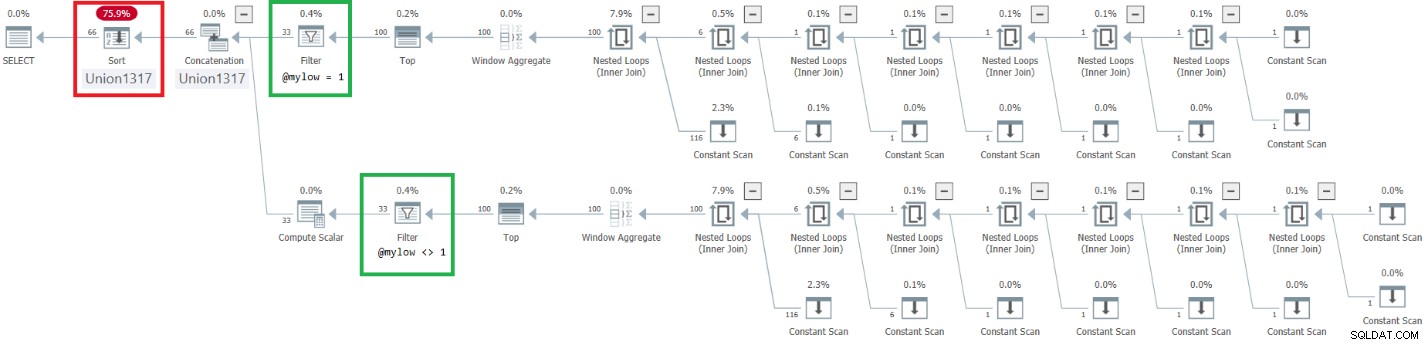Figura 9:Plano para dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) melhorado Observe que o efeito desejado de colocar os operadores Filter acima dos operadores Top foi alcançado. No entanto, a coluna de ordenação n é tratada como resultado de manipulação e, portanto, não é considerada uma coluna que preserva a ordem em relação a rownum. Consequentemente, há uma classificação explícita no plano.
Teste a função com um grande intervalo de 100 milhões de números:
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000; DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
Eu tenho as seguintes estatísticas de tempo:
Tempo de CPU =29907 ms, tempo decorrido =29909 ms.
Que chatice; foi quase perfeito!
Resumo e insights de desempenho
A Figura 10 apresenta um resumo das estatísticas de tempo para as diferentes soluções.
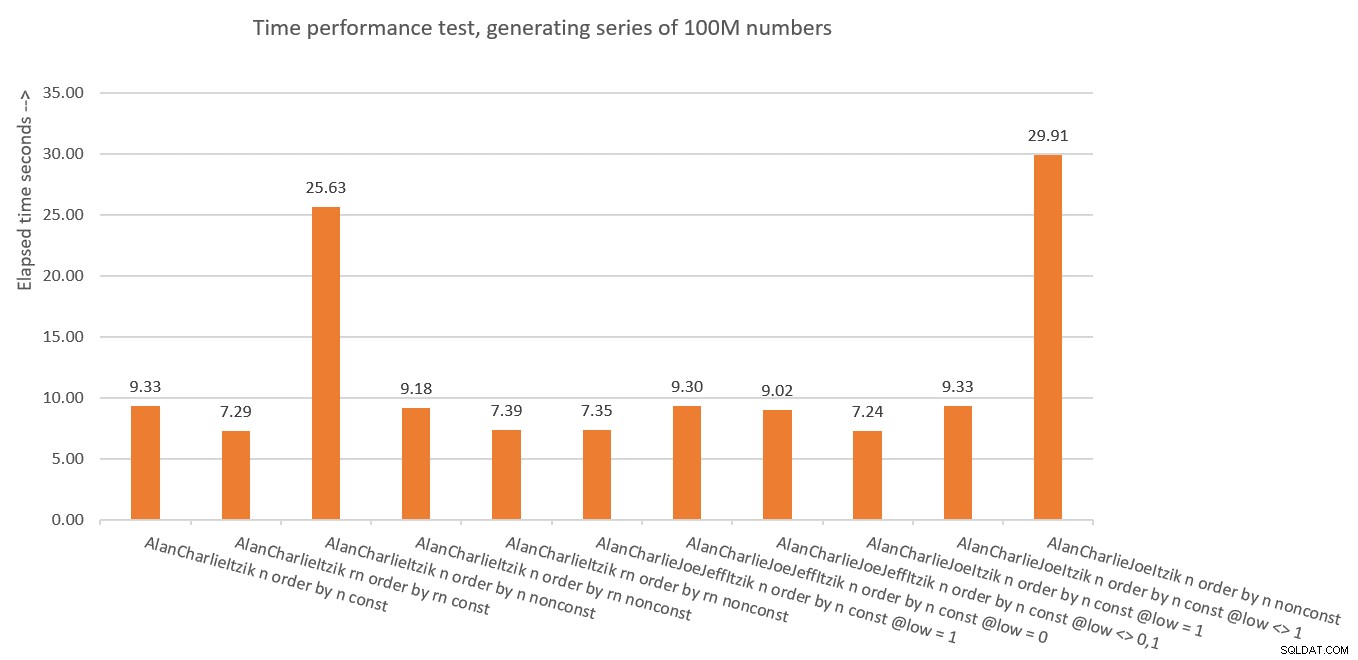Figura 10:Resumo do desempenho de tempo das soluções Então, o que aprendemos com tudo isso? Acho que não vou fazer de novo! Estou brincando. Aprendemos que é mais seguro usar o conceito de eliminação vertical como em dbo.GetNumsAlanCharlieItzikBatch, que expõe tanto o resultado ROW_NUMBER não manipulado (rn) quanto o manipulado (n). Apenas certifique-se de que ao precisar retornar o resultado ordenado, sempre ordene por rn, seja retornando rn ou n.
Se você tem certeza absoluta de que sua solução sempre será usada com constantes como entradas, você pode usar o conceito de eliminação de unidade horizontal. Isso resultará em uma solução mais intuitiva para o usuário, pois ele estará interagindo com uma coluna para os valores crescentes. Eu ainda sugeriria usar o truque com as tabelas derivadas para evitar o desaninhamento e colocar os operadores Filter acima dos operadores Top se a função for usada com entradas não constantes, apenas para garantir.
Ainda não terminamos. No próximo mês, continuarei explorando soluções adicionais.
