Esta é a quarta parte de uma série sobre soluções para o desafio do gerador de séries numéricas. Muito obrigado a Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea e Paul White por compartilhar suas ideias e comentários.
Eu amo o trabalho de Paul White. Fico chocado com suas descobertas e me pergunto como diabos ele descobre o que faz. Também adoro seu estilo de escrita eficiente e eloquente. Muitas vezes, enquanto leio seus artigos ou posts, balanço a cabeça e digo à minha esposa, Lilach, que quando crescer, quero ser como Paul.
Quando publiquei o desafio originalmente, esperava secretamente que Paul publicasse uma solução. Eu sabia que se ele o fizesse, seria muito especial. Bem, ele fez, e é fascinante! Ele tem um desempenho excelente e há muito o que você pode aprender com ele. Este artigo é dedicado à solução de Paul.
Farei meus testes no tempdb, habilitando as estatísticas de I/O e tempo:
SET NOCOUNT ON; USE tempdb; SET STATISTICS TIME, IO ON;
Limitações de ideias anteriores
Avaliando soluções anteriores, um dos fatores importantes para obter um bom desempenho foi a capacidade de empregar processamento em lote. Mas nós a exploramos ao máximo?
Vamos examinar os planos para duas das soluções anteriores que utilizavam processamento em lote. Na Parte 1 abordei a função dbo.GetNumsAlanCharlieItzikBatch, que combinava ideias de Alan, Charlie e eu.
Aqui está a definição da função:
-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Essa solução define um construtor de valor de tabela base com 16 linhas e uma série de CTEs em cascata com junções cruzadas para inflar o número de linhas para potencialmente 4B. A solução usa a função ROW_NUMBER para criar a sequência básica de números em um CTE chamado Nums e o filtro TOP para filtrar a cardinalidade da série numérica desejada. Para habilitar o processamento em lote, a solução usa uma junção esquerda fictícia com uma condição falsa entre o Nums CTE e uma tabela chamada dbo.BatchMe, que possui um índice columnstore.
Use o código a seguir para testar a função com a técnica de atribuição de variável:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
A representação do Plan Explorer do real plano para esta execução é mostrado na Figura 1.
Figura 1:planejar a função dbo.GetNumsAlanCharlieItzikBatch Ao analisar o processamento de modo de lote versus modo de linha, é muito bom poder dizer apenas olhando para um plano em alto nível qual modo de processamento cada operador usou. De fato, o Plan Explorer mostra uma figura de lote azul claro na parte inferior esquerda do operador quando seu modo de execução real é Lote. Como você pode ver na Figura 1, o único operador que usou o modo batch é o operador Window Aggregate, que calcula os números das linhas. Ainda há muito trabalho feito por outros operadores no modo de linha.
Aqui estão os números de desempenho que obtive no meu teste:
Tempo de CPU =10.032 ms, tempo decorrido =10.025 ms.
leituras lógicas 0
Para identificar quais operadores levaram mais tempo para serem executados, use a opção Plano de Execução Real no SSMS ou a opção Obter Plano Real no Plan Explorer. Certifique-se de ler o artigo recente de Paul Understanding Execution Plan Operator Timings. O artigo descreve como normalizar os tempos de execução do operador relatados para obter os números corretos.
No plano da Figura 1, a maior parte do tempo é gasta pelos operadores Nested Loops e Top mais à esquerda, ambos executando no modo de linha. Além de o modo de linha ser menos eficiente que o modo de lote para operações intensivas da CPU, lembre-se de que alternar do modo de linha para o modo de lote e vice-versa exige um custo extra.
Na Parte 2, abordei outra solução que empregava processamento em lote, implementado na função dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Esta solução combinou ideias de John Number2, Dave Mason, Joe Obbish, Alan, Charlie e eu. A principal diferença entre a solução anterior e esta é que, como unidade base, a primeira usa um construtor de valor de tabela virtual e a segunda usa uma tabela real com um índice columnstore, fornecendo processamento em lote “de graça”. Aqui está o código que cria a tabela e a preenche usando uma instrução INSERT com 102.400 linhas para que ela seja compactada:
DROP TABLE IF EXISTS dbo.NullBits102400;
GO
CREATE TABLE dbo.NullBits102400
(
b BIT NULL,
INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b)
SELECT TOP(102400) b FROM nulls;
GO Aqui está a definição da função:
CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
(@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM dbo.NullBits102400 AS A
CROSS JOIN dbo.NullBits102400 AS B)
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO Uma única junção cruzada entre duas instâncias da tabela base é suficiente para produzir muito além do potencial desejado de 4B linhas. Novamente aqui, a solução usa a função ROW_NUMBER para produzir a sequência básica de números e o filtro TOP para restringir a cardinalidade da série numérica desejada.
Aqui está o código para testar a função usando a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);
O plano para esta execução é mostrado na Figura 2.
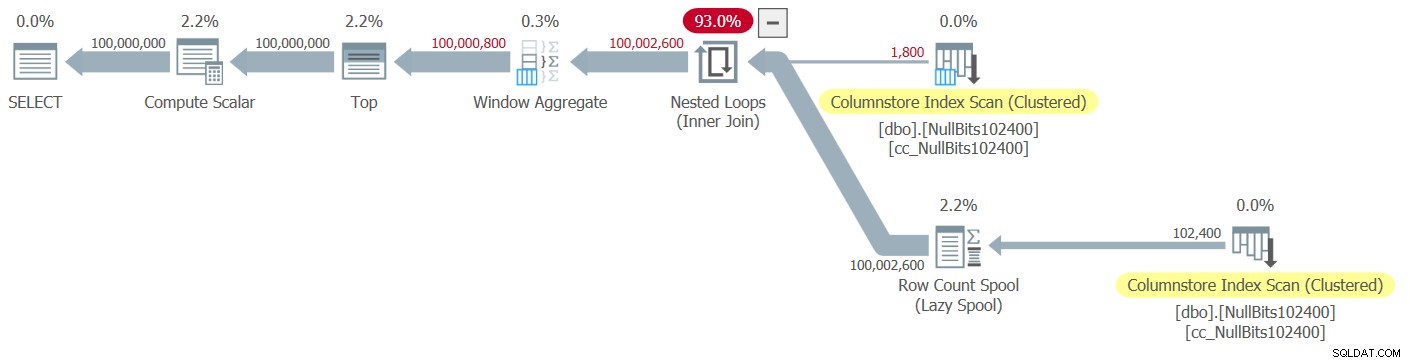Figura 2:planejar a função dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 Observe que apenas dois operadores neste plano utilizam o modo em lote - a varredura superior do índice columnstore clusterizado da tabela, que é usado como a entrada externa da junção de loops aninhados, e o operador Window Aggregate, que é usado para calcular os números de linha base .
Eu obtive os seguintes números de desempenho para o meu teste:
Tempo de CPU =9812 ms, tempo decorrido =9813 ms.
Tabela 'NullBits102400'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 8, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Tabela 'NullBits102400'. O segmento lê 2, segmento ignorado 0.
Novamente, a maior parte do tempo na execução desse plano é gasto pelos operadores Loops e Top mais à esquerda, que são executados no modo de linha.
Solução de Paul
Antes de apresentar a solução de Paul, vou começar com minha teoria sobre o processo de pensamento pelo qual ele passou. Este é realmente um ótimo exercício de aprendizado, e sugiro que você o faça antes de olhar para a solução. Paul reconheceu os efeitos debilitantes de um plano que mistura os modos de lote e de linha, e desafiou-se a encontrar uma solução que obtenha um plano de modo de todos os lotes. Se for bem-sucedida, o potencial para tal solução ter um bom desempenho é bastante alto. Certamente é intrigante ver se esse objetivo é atingível, pois ainda existem muitos operadores que ainda não suportam o modo em lote e muitos fatores que inibem o processamento em lote. Por exemplo, no momento da escrita, o único algoritmo de junção que oferece suporte ao processamento em lote é o algoritmo de junção de hash. Uma junção cruzada é otimizada usando o algoritmo de loops aninhados. Além disso, o operador Top é atualmente implementado apenas no modo de linha. Esses dois elementos são elementos fundamentais críticos usados nos planos de muitas das soluções que abordei até agora, incluindo as duas acima.
Assumindo que você deu ao desafio de criar uma solução com um plano de modo todo em lote uma tentativa decente, vamos prosseguir para o segundo exercício. Primeiro apresentarei a solução de Paul como ele a forneceu, com seus comentários embutidos. Também vou executá-lo para comparar seu desempenho com as outras soluções. Aprendi muito desconstruindo e reconstruindo sua solução, um passo de cada vez, para ter certeza de que entendi cuidadosamente por que ele usou cada uma das técnicas que usou. Sugiro que você faça o mesmo antes de passar a ler minhas explicações.
Aqui está a solução de Paul, que envolve uma tabela columnstore auxiliar chamada dbo.CS e uma função chamada dbo.GetNums_SQLkiwi:
-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
-- type as integer NOT NULL
-- (everything is normalized to 64 bits in columnstore/batch mode anyway)
n1 = ISNULL(CONVERT(integer, 0), 0),
n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
FROM master.dbo.spt_values AS SV1
CROSS JOIN master.dbo.spt_values AS SV2
ORDER BY
rn ASC
OFFSET 0 ROWS
FETCH NEXT 65536 ROWS ONLY
) AS N;
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI
ON dbo.CS
WITH (MAXDOP = 1);
GO
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
-- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
-- Batch mode hash cross join
-- Integer not null data type avoid hash probe residual
-- This is always 0 = 0
ON N2.n1 = N1.n1
WHERE
-- Try to avoid SQRT on negative numbers and enable simplification
-- to single constant scan if @low > @high (with literals)
-- No start-up filters in batch mode
@high >= @low
-- Coarse filter:
-- Limit each side of the cross join to SQRT(target number of rows)
-- IIF avoids SQRT on negative numbers with parameters
AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
) AS N
WHERE
-- Precise filter:
-- Batch mode filter the limited cross join to the exact number of rows needed
-- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
@low - 2 + N.rn < @high;
GO Aqui está o código que usei para testar a função com a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);
Eu obtive o plano mostrado na Figura 3 para o meu teste.
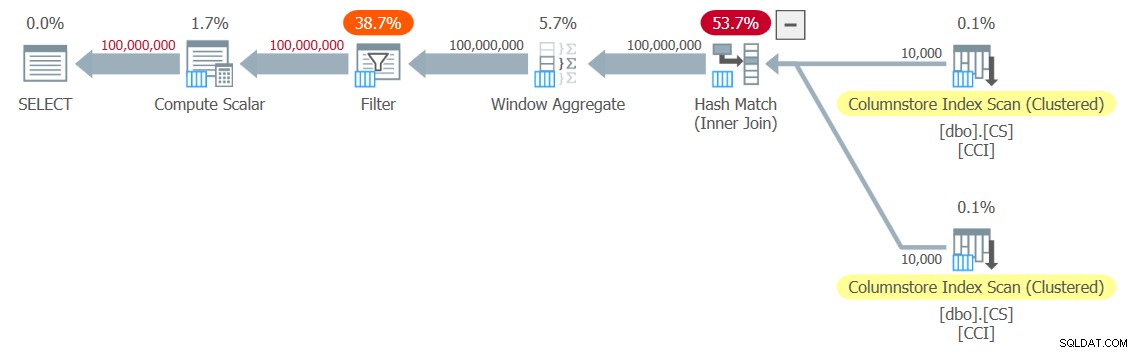Figura 3:planejar a função dbo.GetNums_SQLkiwi É um plano em modo de lote! Isso é bastante impressionante.
Aqui estão os números de desempenho que obtive para este teste na minha máquina:
Tempo de CPU =7812 ms, tempo decorrido =7876 ms.
Tabela 'CS'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 44, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Tabela 'CS'. O segmento lê 2, segmento ignorado 0.
Vamos também verificar se você precisa retornar os números ordenados por n, a solução preserva a ordem em relação a rn—pelo menos ao usar constantes como entradas—e assim evitar a ordenação explícita no plano. Aqui está o código para testá-lo com ordem:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;
Você obtém o mesmo plano da Figura 3 e, portanto, números de desempenho semelhantes:
Tempo de CPU =7765 ms, tempo decorrido =7822 ms.
Tabela 'CS'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 44, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Tabela 'CS'. O segmento lê 2, segmento ignorado 0.
Esse é um lado importante da solução.
Mudando nossa metodologia de teste
O desempenho da solução de Paul é uma melhoria decente tanto no tempo decorrido quanto no tempo de CPU em comparação com as duas soluções anteriores, mas não parece a melhoria mais dramática que se esperaria de um plano de modo todo em lote. Talvez estejamos perdendo alguma coisa?
Vamos tentar analisar os tempos de execução do operador observando o Plano de Execução Real no SSMS, conforme mostrado na Figura 4.
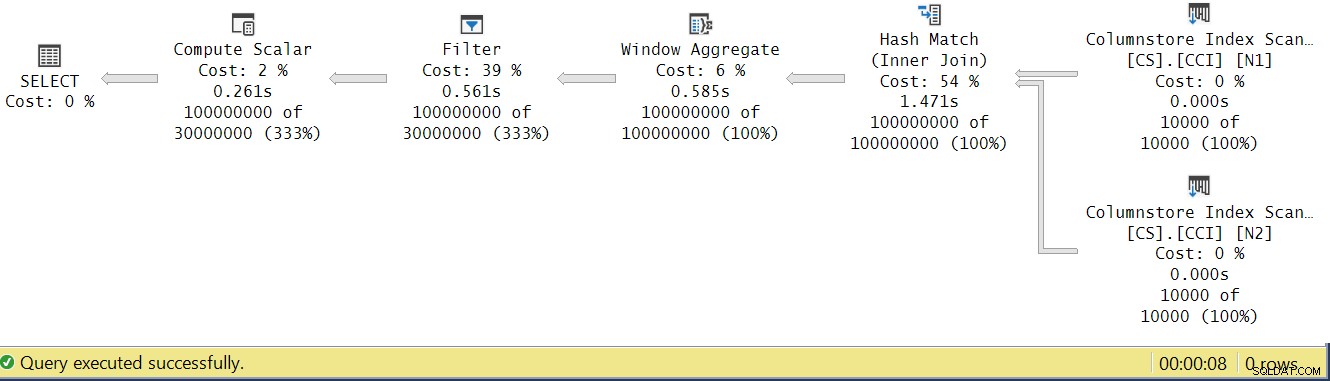Figura 4:Tempos de execução do operador para a função dbo.GetNums_SQLkiwi No artigo de Paul sobre a análise dos tempos de execução do operador, ele explica que, com os operadores de modo de lote, cada um relata seu próprio tempo de execução. Se você somar os tempos de execução de todos os operadores neste plano real, obterá 2,878 segundos, mas o plano levou 7,876 segundos para ser executado. 5 segundos do tempo de execução parecem estar faltando. A resposta para isso está na técnica de teste que estamos usando, com a atribuição de variável. Lembre-se de que decidimos usar essa técnica para eliminar a necessidade de enviar todas as linhas do servidor para o chamador e evitar as E/Ss que estariam envolvidas na gravação do resultado em uma tabela. Parecia a opção perfeita. No entanto, o verdadeiro custo da atribuição de variável está oculto neste plano e, claro, é executado no modo de linha. Mistério resolvido.
Obviamente, no final das contas, um bom teste é um teste que reflete adequadamente o uso da solução em produção. Se você normalmente grava os dados em uma tabela, precisa que seu teste reflita isso. Se você enviar o resultado para o chamador, precisará que seu teste reflita isso. De qualquer forma, a atribuição de variável parece representar uma grande parte do tempo de execução em nosso teste e, claramente, é improvável que represente o uso típico de produção da função. Paul sugeriu que, em vez de atribuição de variável, o teste poderia aplicar uma agregação simples como MAX à coluna numérica retornada (n/rn/op). Um operador agregado pode utilizar o processamento em lote, portanto, o plano não envolveria a conversão do modo de lote para linha como resultado de seu uso, e sua contribuição para o tempo total de execução deve ser bastante pequena e conhecida.
Então, vamos testar novamente todas as três soluções abordadas neste artigo. Aqui está o código para testar a função dbo.GetNumsAlanCharlieItzikBatch:
SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Eu tenho o plano mostrado na Figura 5 para este teste.
Figura 5:planejar a função dbo.GetNumsAlanCharlieItzikBatch com agregação Aqui estão os números de desempenho que obtive para este teste:
Tempo de CPU =8469 ms, tempo decorrido =8733 ms.
leituras lógicas 0
Observe que o tempo de execução caiu de 10,025 segundos usando a técnica de atribuição de variável para 8,733 usando a técnica de agregação. Isso é um pouco mais de um segundo de tempo de execução que podemos atribuir à atribuição de variável aqui.
Aqui está o código para testar a função dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2:
SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);
Eu tenho o plano mostrado na Figura 6 para este teste.
Figura 6:planejar a função dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2 com agregação Aqui estão os números de desempenho que obtive para este teste:
Tempo de CPU =7031 ms, tempo decorrido =7053 ms.
Tabela 'NullBits102400'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 8, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Tabela 'NullBits102400'. O segmento lê 2, segmento ignorado 0.
Observe que o tempo de execução caiu de 9,813 segundos usando a técnica de atribuição de variável para 7,053 usando a técnica de agregação. Isso é um pouco mais de dois segundos de tempo de execução que podemos atribuir à atribuição de variável aqui.
E aqui está o código para testar a solução de Paul:
SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);
Recebo o plano mostrado na Figura 7 para este teste.
Figura 7:planejar a função dbo.GetNums_SQLkiwi com agregação E agora para o grande momento. Eu obtive os seguintes números de desempenho para este teste:
Tempo de CPU =3125 ms, tempo decorrido =3149 ms.
Tabela 'CS'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 44, leitura física lob 0, servidor de página lob lê 0, leitura lob A frente lê 0, a leitura antecipada do servidor de página lob lê 0.
Tabela 'CS'. O segmento lê 2, segmento ignorado 0.
O tempo de execução caiu de 7,822 segundos para 3,149 segundos! Vamos examinar os tempos de execução do operador no plano real no SSMS, conforme mostrado na Figura 8.
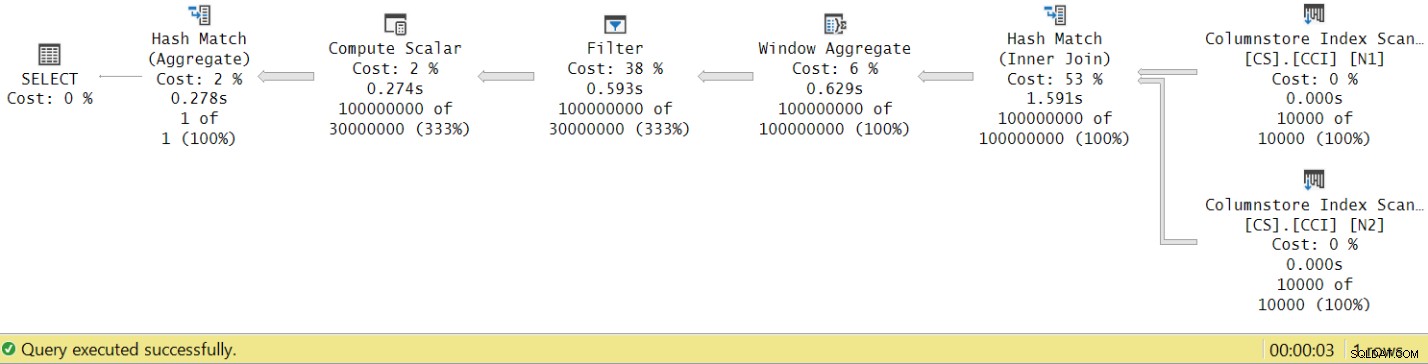Figura 8:tempos de execução do operador para a função dbo.GetNums com agregação Agora, se você acumular os tempos de execução dos operadores individuais, obterá um número semelhante ao tempo total de execução do plano.
A Figura 9 apresenta uma comparação de desempenho em termos de tempo decorrido entre as três soluções usando as técnicas de atribuição de variáveis e de teste agregado.
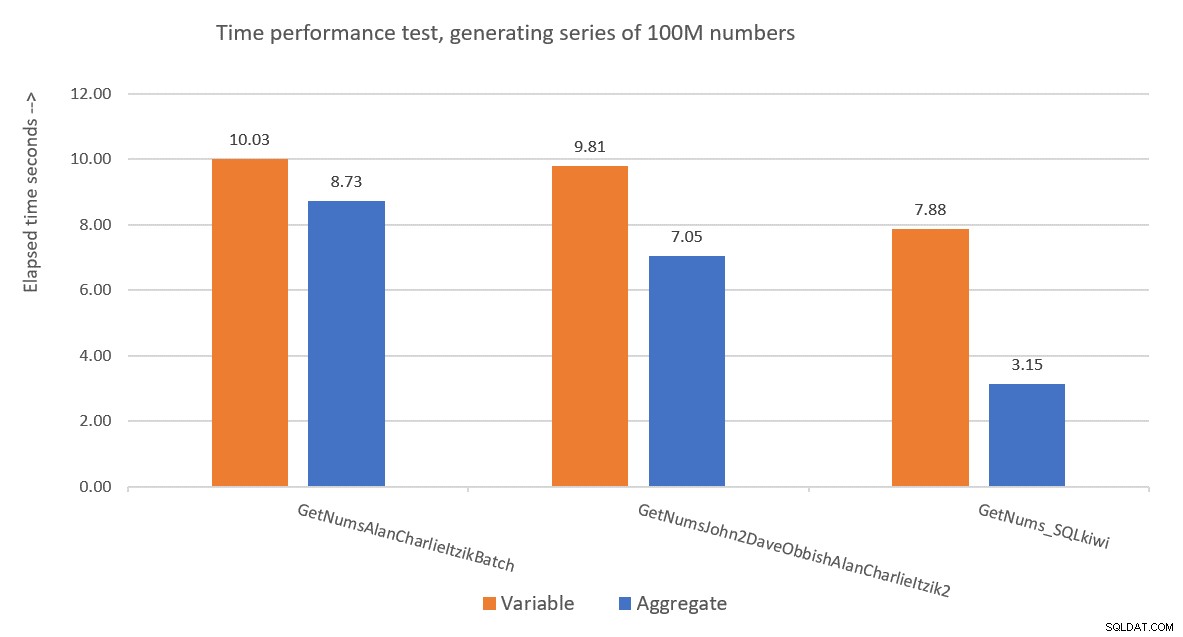Figura 9:comparação de desempenho A solução de Paul é uma vencedora clara, e isso é especialmente aparente ao usar a técnica de teste agregado. Que feito impressionante!
Desconstruindo e reconstruindo a solução de Paul
Desconstruir e reconstruir a solução de Paul é um ótimo exercício, e você aprende muito ao fazê-lo. Como sugerido anteriormente, recomendo que você mesmo passe pelo processo antes de continuar lendo.
A primeira escolha que você precisa fazer é a técnica que você usaria para gerar o número potencial desejado de linhas de 4B. Paul optou por usar uma tabela columnstore e preenchê-la com tantas linhas quanto a raiz quadrada do número necessário, ou seja, 65.536 linhas, para que, com uma única junção cruzada, você obtivesse o número necessário. Talvez você esteja pensando que com menos de 102.400 linhas você não obteria um grupo de linhas compactado, mas isso se aplica ao preencher a tabela com uma instrução INSERT como fizemos com a tabela dbo.NullBits102400. Não se aplica quando você cria um índice columnstore em uma tabela pré-preenchida. Então, Paul usou uma instrução SELECT INTO para criar e preencher a tabela como um heap baseado em rowstore com 65.536 linhas e, em seguida, criou um índice columnstore clusterizado, resultando em um grupo de linhas compactado.
O próximo desafio é descobrir como fazer com que uma junção cruzada seja processada com um operador de modo de lote. Para isso, você precisa que o algoritmo de junção seja hash. Lembre-se de que uma junção cruzada é otimizada usando o algoritmo de loops aninhados. De alguma forma, você precisa enganar o otimizador para pensar que está usando um equijoin interno (o hash requer pelo menos um predicado baseado em igualdade), mas obtenha uma junção cruzada na prática.
Uma primeira tentativa óbvia é usar uma junção interna com um predicado de junção artificial que é sempre verdadeiro, assim:
SELECT *
FROM dbo.CS AS N1
INNER HASH JOIN dbo.CS AS N2
ON 0 = 0; Mas este código falha com o seguinte erro:
Msg 8622, Level 16, State 1, Line 246
O processador de consulta não pôde produzir um plano de consulta devido às dicas definidas nesta consulta. Reenvie a consulta sem especificar nenhuma dica e sem usar SET FORCEPLAN.
O otimizador do SQL Server reconhece que este é um predicado artificial de junção interna, simplifica a junção interna para uma junção cruzada e produz um erro informando que não pode acomodar a dica para forçar um algoritmo de junção de hash.
Para resolver isso, Paul criou uma coluna INT NOT NULL (mais sobre por que essa especificação em breve) chamada n1 em sua tabela dbo.CS e a preencheu com 0 em todas as linhas. Ele então usou o predicado de junção N2.n1 =N1.n1, obtendo efetivamente a proposição 0 =0 em todas as avaliações de correspondência, enquanto cumpria os requisitos mínimos para um algoritmo de junção de hash.
Isso funciona e produz um plano em modo de lote:
SELECT *
FROM dbo.CS AS N1
INNER HASH JOIN dbo.CS AS N2
ON N2.n1 = N1.n1; Quanto ao motivo de n1 ser definido como INT NOT NULL; por que não permitir NULLs e por que não usar BIGINT? O motivo dessas escolhas é evitar um resíduo de sondagem de hash (um filtro extra que é aplicado pelo operador de junção de hash além do predicado de junção original), o que pode resultar em um custo extra desnecessário. Veja o artigo de Paul Join Performance, Implicit Conversions, and Residuals para mais detalhes. Aqui está a parte do artigo que é relevante para nós:
"Se a junção estiver em uma única coluna digitada como tinyint, smallint ou integer e se ambas as colunas forem restritas a NOT NULL, a função de hash será 'perfeita' - significando que não há chance de uma colisão de hash e o processador de consulta não precisa verificar os valores novamente para garantir que eles realmente correspondam.
Observe que essa otimização não se aplica a colunas bigint."
Para verificar esse aspecto, vamos criar outra tabela chamada dbo.CS2 com uma coluna n1 anulável:
DROP TABLE IF EXISTS dbo.CS2; SELECT * INTO dbo.CS2 FROM dbo.CS; ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL; CREATE CLUSTERED COLUMNSTORE INDEX CCI ON dbo.CS2 WITH (MAXDOP = 1);
Vamos primeiro testar uma consulta em relação a dbo.CS (onde n1 é definido como INT NOT NULL), gerando 4B números de linha base em uma coluna chamada rn e aplicando o agregado MAX à coluna:
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
) AS N; Vamos comparar o plano para esta consulta com o plano para uma consulta semelhante em relação a dbo.CS2 (onde n1 é definido como INT NULL):
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS2 AS N1
JOIN dbo.CS2 AS N2
ON N2.n1 = N1.n1
) AS N; Os planos para ambas as consultas são mostrados na Figura 10.
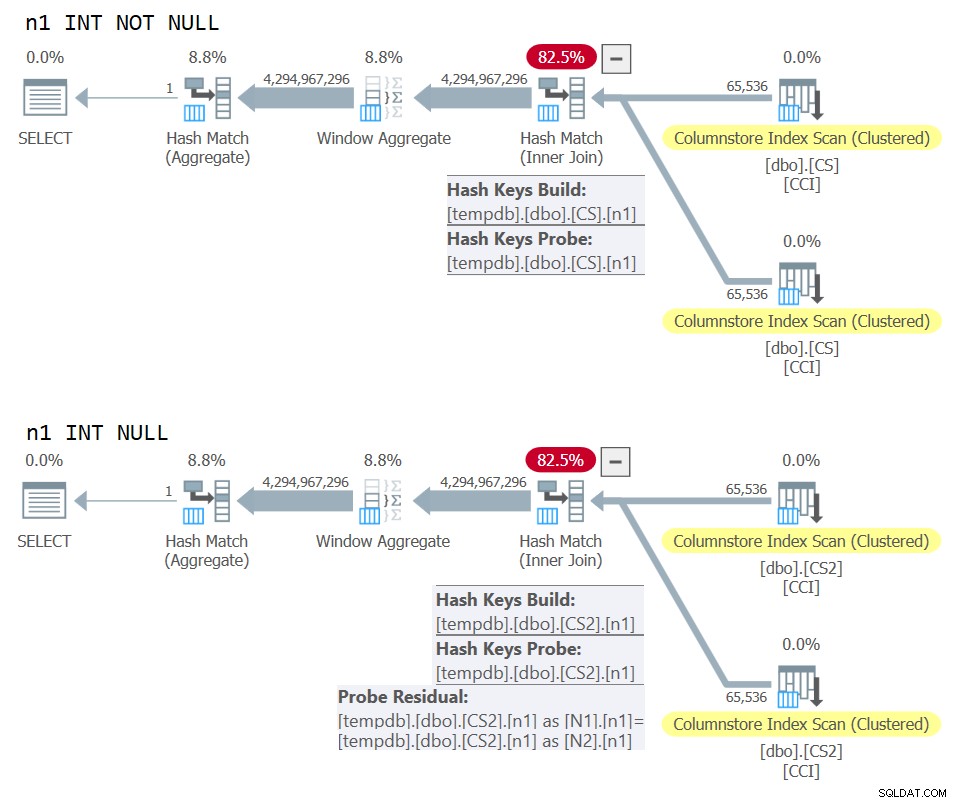Figura 10:Comparação de planos para chave de junção NOT NULL vs NULL Você pode ver claramente o resíduo de sonda extra que é aplicado no segundo plano, mas não no primeiro.
Na minha máquina, a consulta ao dbo.CS foi concluída em 91 segundos e a consulta ao dbo.CS2 foi concluída em 92 segundos. No artigo de Paul, ele relata uma diferença de 11% a favor do caso NOT NULL para o exemplo que ele usou.
BTW, aqueles de vocês com um olho afiado notaram o uso de ORDER BY @@TRANCOUNT como a especificação de pedido da função ROW_NUMBER. Se você ler atentamente os comentários inline de Paul em sua solução, ele menciona que o uso da função @@TRANCOUNT é um inibidor de paralelismo, enquanto o uso de @@SPID não é. Portanto, você pode usar @@TRANCOUNT como a constante de tempo de execução na especificação de pedido quando quiser forçar um plano serial e @@SPID quando não quiser.
Como mencionado, a consulta ao dbo.CS levou 91 segundos para ser executada na minha máquina. Neste ponto, pode ser interessante testar o mesmo código com uma junção cruzada verdadeira, permitindo que o otimizador use um algoritmo de junção de loops aninhados no modo de linha:
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
CROSS JOIN dbo.CS AS N2
) AS N; Este código levou 104 segundos para ser concluído na minha máquina. Portanto, obtemos uma melhoria de desempenho considerável com a junção de hash em modo de lote.
Nosso próximo problema é o fato de que, ao usar TOP para filtrar o número desejado de linhas, você obtém um plano com um operador Top no modo de linha. Aqui está uma tentativa de implementar a função dbo.GetNums_SQLkiwi com um filtro TOP:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT TOP (100000000 - 1 + 1)
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
ORDER BY rn
) AS N;
GO Vamos testar a função:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
Eu obtive o plano mostrado na Figura 11 para este teste.
Figura 11:Plano com filtro TOP Observe que o operador Top é o único no plano que usa processamento em modo de linha.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =6078 ms, tempo decorrido =6071 ms.
A maior parte do tempo de execução neste plano é gasto pelo operador Top do modo de linha e pelo fato de que o plano precisa passar pela conversão de lote para modo de linha e vice-versa.
Nosso desafio é descobrir uma alternativa de filtragem em modo de lote para o modo de linha TOP. Filtros baseados em predicados, como os aplicados com a cláusula WHERE, podem potencialmente ser tratados com processamento em lote.
A abordagem de Paul foi introduzir uma segunda coluna do tipo INT (veja o comentário embutido “tudo é normalizado para 64 bits no modo columnstore/batch de qualquer maneira” ) chamou n2 para a tabela dbo.CS e a preencheu com a sequência inteira de 1 a 65.536. No código da solução ele usou dois filtros baseados em predicados. Um é um filtro grosseiro na consulta interna com predicados envolvendo a coluna n2 de ambos os lados da junção. Este filtro grosseiro pode resultar em alguns falsos positivos. Aqui está a primeira tentativa simplista de tal filtro:
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1)))) Com as entradas 1 e 100.000.000 como @low e @high, você não obtém falsos positivos. Mas tente com 1 e 100.000.001, e você consegue alguns. Você obterá uma sequência de 100.020.001 números em vez de 100.000.001.
Para eliminar os falsos positivos, Paul adicionou um segundo filtro preciso envolvendo a coluna rn na consulta externa. Aqui está a primeira tentativa simplista de um filtro tão preciso:
WHERE
-- Precise filter:
N.rn < @high - @low + 2 Vamos revisar a definição da função para usar os filtros baseados em predicados acima em vez de TOP, pegue 1:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
) AS N
WHERE
-- Precise filter:
N.rn < @high - @low + 2;
GO Vamos testar a função:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
Eu obtive o plano mostrado na Figura 12 para este teste.
Figura 12:Planeje com o filtro WHERE, faça 1 Infelizmente, algo claramente deu errado. O SQL Server converteu nosso filtro baseado em predicado envolvendo a coluna rn em um filtro baseado em TOP e o otimizou com um operador Top — exatamente o que tentamos evitar. Para adicionar insulto à injúria, o otimizador também decidiu usar o algoritmo de loops aninhados para a junção.
Este código levou 18,8 segundos para terminar na minha máquina. Não parece bom.
Em relação à junção de loops aninhados, isso é algo que poderíamos facilmente resolver usando uma dica de junção na consulta interna. Apenas para ver o impacto no desempenho, aqui está um teste com uma dica de consulta de junção de hash forçada usada na própria consulta de teste:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);
O tempo de execução é reduzido para 13,2 segundos.
Ainda temos o problema com a conversão do filtro WHERE contra rn para um filtro TOP. Vamos tentar entender como isso aconteceu. Usamos o seguinte filtro na consulta externa:
WHERE N.rn < @high - @low + 2
Lembre-se de que rn representa uma expressão baseada em ROW_NUMBER não manipulada. Um filtro baseado em uma expressão não manipulada em um determinado intervalo geralmente é otimizado com um operador Top, o que para nós é uma má notícia devido ao uso de processamento em modo de linha.
A solução de Paul era usar um predicado equivalente, mas que aplicasse manipulação a rn, assim:
WHERE @low - 2 + N.rn < @high
Filtrar uma expressão que adiciona manipulação a uma expressão baseada em ROW_NUMBER inibe a conversão do filtro baseado em predicado em um baseado em TOP. Isso é brilhante!
Vamos revisar a definição da função para usar o predicado WHERE acima, pegue 2:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
) AS N
WHERE
-- Precise filter:
@low - 2 + N.rn < @high;
GO Test the function again, without any special hints or anything:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
It naturally gets an all-batch-mode plan with a hash join algorithm and no Top operator, resulting in an execution time of 3.177 seconds. Looking good.
The next step is to check if the solution handles bad inputs well. Let’s try it with a negative delta:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);
This execution fails with the following error.
Msg 3623, Level 16, State 1, Line 436
An invalid floating point operation occurred.
The failure is due to the attempt to apply a square root of a negative number.
Paul’s solution involved two additions. One is to add the following predicate to the inner query’s WHERE clause:
@high >= @low
This filter does more than what it seems initially. If you’ve read Paul’s inline comments carefully, you could find this part:
“Try to avoid SQRT on negative numbers and enable simplification to single constant scan if @low> @high (with literals). No start-up filters in batch mode.”
The intriguing part here is the potential to use a constant scan with constants as inputs. I’ll get to this shortly.
The other addition is to apply the IIF function to the input expression to the SQRT function. This is done to avoid negative input when using nonconstants as inputs to our numbers function, and in case the optimizer decides to handle the predicate involving SQRT before the predicate @high>=@low.
Before the IIF addition, for example, the predicate involving N1.n2 looked like this:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
After adding IIF, it looks like this:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
-- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
-- Batch mode hash cross join
-- Integer not null data type avoid hash probe residual
-- This is always 0 = 0
ON N2.n1 = N1.n1
WHERE
-- Try to avoid SQRT on negative numbers and enable simplification
-- to single constant scan if @low > @high (with literals)
-- No start-up filters in batch mode
@high >= @low
-- Coarse filter:
-- Limit each side of the cross join to SQRT(target number of rows)
-- IIF avoids SQRT on negative numbers with parameters
AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
) AS N
WHERE
-- Precise filter:
-- Batch mode filter the limited cross join to the exact number of rows needed
-- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
@low - 2 + N.rn < @high;
GO Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:
WHERE
1 >= 100000000
AND ... The whole plan can then be simplified to a single Constant Scan operator. Tente:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);
The plan for this execution is shown in Figure 13.
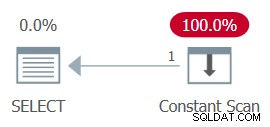Figure 13:Plan with constant scan Unsurprisingly, I got the following performance numbers for this execution:
CPU time =0 ms, elapsed time =0 ms.
logical reads 0
When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.
Now let’s test the function with a valid input range:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
You get the all-batch-mode plan shown in Figure 14.
Figure 14:Plan for dbo.GetNums_SQLkiwi function This is the same plan you saw earlier in Figure 7.
I got the following time statistics for this execution:
CPU time =3000 ms, elapsed time =3111 ms.
Ladies and gentlemen, I think we have a winner! :)
Conclusão
I’ll have what Paul’s having.
Are we done yet, or is this series going to last forever?
No and no.
