Esta é a quinta e última parte da série que abrange soluções para o desafio do gerador de séries numéricas. Na Parte 1, Parte 2, Parte 3 e Parte 4, abordei soluções T-SQL puras. Logo no início, quando postei o quebra-cabeça, várias pessoas comentaram que a solução com melhor desempenho provavelmente seria baseada em CLR. Neste artigo, testaremos essa suposição intuitiva. Especificamente, abordarei soluções baseadas em CLR postadas por Kamil Kosno e Adam Machanic.
Muito obrigado a Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea e Paul White por compartilhar suas ideias e comentários.
Vou fazer meus testes em um banco de dados chamado testdb. Use o código a seguir para criar o banco de dados, caso ele não exista, e para habilitar as estatísticas de E/S e de tempo:
-- DB and stats
SET NOCOUNT ON;
SET STATISTICS IO, TIME ON;
GO
IF DB_ID('testdb') IS NULL CREATE DATABASE testdb;
GO
USE testdb;
GO Para simplificar, desabilitarei a segurança estrita do CLR e tornarei o banco de dados confiável usando o seguinte código:
-- Enable CLR, disable CLR strict security and make db trustworthy EXEC sys.sp_configure 'show advanced settings', 1; RECONFIGURE; EXEC sys.sp_configure 'clr enabled', 1; EXEC sys.sp_configure 'clr strict security', 0; RECONFIGURE; EXEC sys.sp_configure 'show advanced settings', 0; RECONFIGURE; ALTER DATABASE testdb SET TRUSTWORTHY ON; GO
Soluções anteriores
Antes de abordar as soluções baseadas em CLR, vamos analisar rapidamente o desempenho de duas das soluções T-SQL de melhor desempenho.
A solução T-SQL de melhor desempenho que não usou nenhuma tabela base persistente (além da tabela columnstore vazia fictícia para obter processamento em lote) e, portanto, não envolveu operações de E/S, foi aquela implementada na função dbo.GetNumsAlanCharlieItzikBatch. Eu cobri esta solução na Parte 1.
Aqui está o código para criar a tabela columnstore vazia fictícia que a consulta da função usa:
DROP TABLE IF EXISTS dbo.BatchMe; GO CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE); GO
E aqui está o código com a definição da função:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Vamos primeiro testar a função solicitando uma série de 100 milhões de números, com o agregado MAX aplicado à coluna n:
SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Lembre-se, essa técnica de teste evita a transmissão de 100 milhões de linhas para o chamador e também evita o esforço do modo de linha envolvido na atribuição de variáveis ao usar a técnica de atribuição de variáveis.
Aqui estão as estatísticas de tempo que obtive para este teste na minha máquina:
Tempo de CPU =6719 ms, tempo decorrido =6742 ms .
A execução desta função não produz nenhuma leitura lógica, é claro.
Em seguida, vamos testá-lo com ordem, usando a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =9.468 ms, tempo decorrido =9.531 ms .
Lembre-se que esta função não resulta em ordenação ao solicitar os dados ordenados por n; você basicamente obtém o mesmo plano, independentemente de solicitar os dados solicitados ou não. Podemos atribuir a maior parte do tempo extra neste teste em comparação com o anterior às atribuições de variáveis baseadas no modo de linha de 100 milhões.
A solução T-SQL de melhor desempenho que usou uma tabela base persistente e, portanto, resultou em algumas operações de E/S, embora muito poucas, foi a solução de Paul White implementada na função dbo.GetNums_SQLkiwi. Eu cobri esta solução na Parte 4.
Aqui está o código de Paul para criar a tabela columnstore usada pela função e a própria função:
-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
-- type as integer NOT NULL
-- (everything is normalized to 64 bits in columnstore/batch mode anyway)
n1 = ISNULL(CONVERT(integer, 0), 0),
n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
FROM master.dbo.spt_values AS SV1
CROSS JOIN master.dbo.spt_values AS SV2
ORDER BY
rn ASC
OFFSET 0 ROWS
FETCH NEXT 65536 ROWS ONLY
) AS N;
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI
ON dbo.CS
WITH (MAXDOP = 1);
GO
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
-- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
-- Batch mode hash cross join
-- Integer not null data type avoid hash probe residual
-- This is always 0 = 0
ON N2.n1 = N1.n1
WHERE
-- Try to avoid SQRT on negative numbers and enable simplification
-- to single constant scan if @low > @high (with literals)
-- No start-up filters in batch mode
@high >= @low
-- Coarse filter:
-- Limit each side of the cross join to SQRT(target number of rows)
-- IIF avoids SQRT on negative numbers with parameters
AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
) AS N
WHERE
-- Precise filter:
-- Batch mode filter the limited cross join to the exact number of rows needed
-- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
@low - 2 + N.rn < @high;
GO Vamos primeiro testá-lo sem ordem usando a técnica de agregação, resultando em um plano de modo all-batch:
SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);
Eu tenho as seguintes estatísticas de tempo e E/S para esta execução:
Tempo de CPU =2922 ms, tempo decorrido =2943 ms .
Tabela 'CS'. Contagem de varredura 2, leitura lógica 0, leitura física 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, lob leitura lógica 44 , o lob físico lê 0, o servidor de página lob lê 0, a leitura antecipada do lob lê 0, a leitura antecipada do servidor da página lob lê 0.
Tabela 'CS'. O segmento lê 2, segmento ignorado 0.
Vamos testar a função com ordem usando a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
Como na solução anterior, também esta solução evita a classificação explícita no plano e, portanto, obtém o mesmo plano, independentemente de você solicitar os dados solicitados ou não. Mas, novamente, esse teste incorre em uma penalidade extra principalmente devido à técnica de atribuição de variável usada aqui, resultando na parte de atribuição de variável no plano sendo processada no modo de linha.
Aqui estão as estatísticas de tempo e E/S que obtive para esta execução:
Tempo de CPU =6985 ms, tempo decorrido =7033 ms .
Tabela 'CS'. Contagem de varredura 2, leituras lógicas 0, leituras físicas 0, servidor de página lê 0, leitura antecipada lê 0, leitura antecipada do servidor de página lê 0, leitura lógica lob 44 , o lob físico lê 0, o servidor de página lob lê 0, a leitura antecipada do lob lê 0, a leitura antecipada do servidor da página lob lê 0.
Tabela 'CS'. O segmento lê 2, segmento ignorado 0.
Soluções CLR
Ambos Kamil Kosno e Adam Machanic forneceram primeiro uma solução simples somente CLR e, posteriormente, criaram uma combinação CLR + T-SQL mais sofisticada. Começarei com as soluções de Kamil e depois cobrirei as soluções de Adam.
Soluções de Kamil Kosno
Aqui está o código CLR usado na primeira solução de Kamil para definir uma função chamada GetNums_KamilKosno1:
using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsKamil1
{
[Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName = "GetNums_KamilKosno1_Fill", TableDefinition = "n BIGINT")]
public static IEnumerator GetNums_KamilKosno1(SqlInt64 low, SqlInt64 high)
{
return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) : new GetNumsCS(low.Value, high.Value);
}
public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n)
{
n = (long)o;
}
private class GetNumsCS : IEnumerator
{
public GetNumsCS(long from, long to)
{
_lowrange = from;
_current = _lowrange - 1;
_highrange = to;
}
public bool MoveNext()
{
_current += 1;
if (_current > _highrange) return false;
else return true;
}
public object Current
{
get
{
return _current;
}
}
public void Reset()
{
_current = _lowrange - 1;
}
long _lowrange;
long _current;
long _highrange;
}
} A função aceita duas entradas chamadas baixa e alta e retorna uma tabela com uma coluna BIGINT chamada n. A função é um tipo de streaming, retornando uma linha com o próximo número na série por solicitação de linha da consulta de chamada. Como você pode ver, Kamil escolheu o método mais formalizado de implementação da interface IEnumerator, que envolve a implementação dos métodos MoveNext (avança o enumerador para obter a próxima linha), Current (obtém a linha na posição atual do enumerador) e Reset (configura o enumerador para sua posição inicial, que está antes da primeira linha).
A variável que contém o número atual na série é chamada _current. O construtor define _current para o limite inferior do intervalo solicitado menos 1, e o mesmo vale para o método Reset. O método MoveNext avança _current em 1. Então, se _current for maior que o limite superior do intervalo solicitado, o método retornará false, significando que não será chamado novamente. Caso contrário, retorna true, o que significa que será chamado novamente. O método Current retorna naturalmente _current. Como você pode ver, lógica bastante básica.
Chamei o projeto do Visual Studio GetNumsKamil1 e usei o caminho C:\Temp\ para ele. Aqui está o código que usei para implantar a função no banco de dados testdb:
DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno1; DROP ASSEMBLY IF EXISTS GetNumsKamil1; GO CREATE ASSEMBLY GetNumsKamil1 FROM 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll'; GO CREATE FUNCTION dbo.GetNums_KamilKosno1(@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE(n BIGINT) ORDER(n) AS EXTERNAL NAME GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1; GO
Observe o uso da cláusula ORDER na instrução CREATE FUNCTION. A função emite as linhas em n ordenação, portanto, quando as linhas precisam ser ingeridas no plano em n ordenação, com base nessa cláusula o SQL Server sabe que pode evitar uma classificação no plano.
Vamos testar a função, primeiro com a técnica de agregação, quando a ordenação não for necessária:
SELECT MAX(n) AS mx FROM dbo.GetNums_KamilKosno1(1, 100000000);
Eu tenho o plano mostrado na Figura 1.
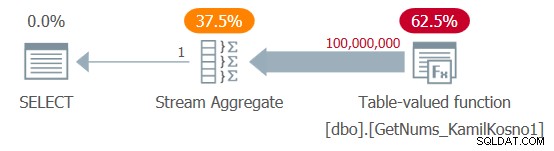Figura 1:planejar a função dbo.GetNums_KamilKosno1 Não há muito a dizer sobre esse plano, além do fato de que todos os operadores usam o modo de execução de linha.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =37375 ms, tempo decorrido =37488 ms .
E, claro, nenhuma leitura lógica estava envolvida.
Vamos testar a função com ordem, usando a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_KamilKosno1(1, 100000000) ORDER BY n;
Eu tenho o plano mostrado na Figura 2 para esta execução.
Figura 2:Planeje a função dbo.GetNums_KamilKosno1 com ORDER BY Observe que não há classificação no plano, pois a função foi criada com a cláusula ORDER(n). No entanto, há algum esforço para garantir que as linhas sejam realmente emitidas da função na ordem prometida. Isso é feito usando os operadores Segment e Sequence Project, que são usados para calcular números de linha, e o operador Assert, que interrompe a execução da consulta se o teste falhar. Este trabalho tem escala linear - ao contrário da escala n log n que você teria obtido se uma classificação fosse necessária - mas ainda não é barato. Eu obtive as seguintes estatísticas de tempo para este teste:
Tempo de CPU =51.531 ms, tempo decorrido =51.905 ms .
Os resultados podem ser surpreendentes para alguns, especialmente para aqueles que intuitivamente presumiram que as soluções baseadas em CLR teriam um desempenho melhor do que as T-SQL. Como você pode ver, os tempos de execução são uma ordem de magnitude maior do que com nossa solução T-SQL de melhor desempenho.
A segunda solução da Kamil é um híbrido CLR-T-SQL. Além das entradas baixa e alta, a função CLR (GetNums_KamilKosno2) adiciona uma entrada de passo e retorna valores entre baixo e alto que estão separados um do outro. Aqui está o código CLR que Kamil usou em sua segunda solução:
using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsKamil2
{
[Microsoft.SqlServer.Server.SqlFunction(DataAccess = Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic = true, IsPrecise = true, FillRowMethodName = "GetNums_Fill", TableDefinition = "n BIGINT")]
public static IEnumerator GetNums_KamilKosno2(SqlInt64 low, SqlInt64 high, SqlInt64 step)
{
return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) : new GetNumsCS(low.Value, high.Value, step.Value);
}
public static void GetNums_Fill(Object o, out SqlInt64 n)
{
n = (long)o;
}
private class GetNumsCS : IEnumerator
{
public GetNumsCS(long from, long to, long step)
{
_lowrange = from;
_step = step;
_current = _lowrange - _step;
_highrange = to;
}
public bool MoveNext()
{
_current = _current + _step;
if (_current > _highrange) return false;
else return true;
}
public object Current
{
get
{
return _current;
}
}
public void Reset()
{
_current = _lowrange - _step;
}
long _lowrange;
long _current;
long _highrange;
long _step;
}
} Denominei o projeto VS GetNumsKamil2, coloquei-o no caminho C:\Temp\ também e usei o seguinte código para implantá-lo no banco de dados testdb:
-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno2;
DROP ASSEMBLY IF EXISTS GetNumsKamil2;
GO
CREATE ASSEMBLY GetNumsKamil2
FROM 'C:\Temp\GetNumsKamil2\GetNumsKamil2\bin\Debug\GetNumsKamil2.dll';
GO
CREATE FUNCTION dbo.GetNums_KamilKosno2
(@low AS BIGINT = 1, @high AS BIGINT, @step AS BIGINT)
RETURNS TABLE(n BIGINT)
ORDER(n)
AS EXTERNAL NAME GetNumsKamil2.GetNumsKamil2.GetNums_KamilKosno2;
GO Como exemplo de uso da função, aqui está uma solicitação para gerar valores entre 5 e 59, com um passo de 10:
SELECT n FROM dbo.GetNums_KamilKosno2(5, 59, 10);
Este código gera a seguinte saída:
n --- 5 15 25 35 45 55
Quanto à parte T-SQL, Kamil utilizou uma função chamada dbo.GetNums_Hybrid_Kamil2, com o seguinte código:
CREATE OR ALTER FUNCTION dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
SELECT TOP (@high - @low + 1) V.n
FROM dbo.GetNums_KamilKosno2(@low, @high, 10) AS GN
CROSS APPLY (VALUES(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n),
(5+GN.n),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);
GO Como você pode ver, a função T-SQL invoca a função CLR com as mesmas entradas @low e @high que obtém e, neste exemplo, usa um tamanho de etapa de 10. A consulta usa CROSS APPLY entre o resultado da função CLR e um construtor de valor de tabela que gera os números finais adicionando valores no intervalo de 0 a 9 ao início da etapa. O filtro TOP é usado para garantir que você não obtenha mais do que o número de números solicitados.
Importante: Devo enfatizar que Kamil faz uma suposição aqui sobre o filtro TOP ser aplicado com base na ordenação do número do resultado, o que não é realmente garantido, pois a consulta não possui uma cláusula ORDER BY. Se você adicionar uma cláusula ORDER BY para dar suporte a TOP ou substituir TOP por um filtro WHERE, para garantir um filtro determinístico, isso poderá alterar completamente o perfil de desempenho da solução.
De qualquer forma, vamos primeiro testar a função sem ordem usando a técnica de agregação:
SELECT MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);
Eu tenho o plano mostrado na Figura 3 para esta execução.
Figura 3:planejar a função dbo.GetNums_Hybrid_Kamil2 Novamente, todos os operadores no plano usam o modo de execução de linha.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =13985 ms, tempo decorrido =14069 ms .
E, naturalmente, nenhuma leitura lógica.
Vamos testar a função com ordem:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000) ORDER BY n;
Eu tenho o plano mostrado na Figura 4.
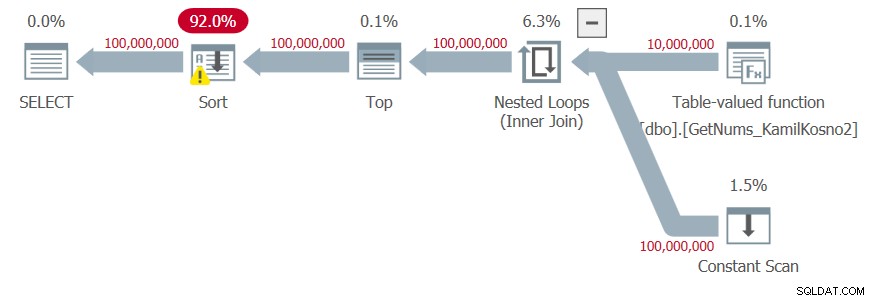Figura 4:planejar a função dbo.GetNums_Hybrid_Kamil2 com ORDER BY Como os números de resultado são o resultado da manipulação do limite inferior da etapa retornada pela função CLR e o delta adicionado no construtor de valor de tabela, o otimizador não confia que os números de resultado sejam gerados na ordem solicitada e adiciona classificação explícita ao plano.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =68703 ms, tempo decorrido =84538 ms .
Então, parece que quando nenhuma ordem é necessária, a segunda solução de Kamil se sai melhor que a primeira. Mas quando a ordem é necessária, é o contrário. De qualquer forma, as soluções T-SQL são mais rápidas. Pessoalmente, eu confiaria na correção da primeira solução, mas não na segunda.
Soluções de Adam Machanic
A primeira solução de Adam também é uma função CLR básica que continua incrementando um contador. Só que em vez de usar a abordagem formalizada mais envolvida como Kamil fez, Adam usou uma abordagem mais simples que invoca o comando yield por linha que precisa ser retornada.
Aqui está o código CLR de Adam para sua primeira solução, definindo uma função de streaming chamada GetNums_AdamMachanic1:
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsAdam1
{
[Microsoft.SqlServer.Server.SqlFunction(
FillRowMethodName = "GetNums_AdamMachanic1_fill",
TableDefinition = "n BIGINT")]
public static IEnumerable GetNums_AdamMachanic1(SqlInt64 min, SqlInt64 max)
{
var min_int = min.Value;
var max_int = max.Value;
for (; min_int <= max_int; min_int++)
{
yield return (min_int);
}
}
public static void GetNums_AdamMachanic1_fill(object o, out long i)
{
i = (long)o;
}
}; A solução é tão elegante em sua simplicidade. Como você pode ver, a função aceita duas entradas chamadas min e max representando os pontos de limite inferior e superior do intervalo solicitado e retorna uma tabela com uma coluna BIGINT chamada n. A função inicializa variáveis chamadas min_int e max_int com os respectivos valores de parâmetro de entrada da função. A função então executa um loop enquanto min_int <=max_int, que em cada iteração produz uma linha com o valor atual de min_int e incrementa min_int em 1. É isso.
Chamei o projeto GetNumsAdam1 no VS, coloquei-o em C:\Temp\ e usei o seguinte código para implantá-lo:
-- Create assembly and function DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic1; DROP ASSEMBLY IF EXISTS GetNumsAdam1; GO CREATE ASSEMBLY GetNumsAdam1 FROM 'C:\Temp\GetNumsAdam1\GetNumsAdam1\bin\Debug\GetNumsAdam1.dll'; GO CREATE FUNCTION dbo.GetNums_AdamMachanic1(@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE(n BIGINT) ORDER(n) AS EXTERNAL NAME GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1; GO
Usei o seguinte código para testá-lo com a técnica de agregação, para casos em que a ordem não importa:
SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic1(1, 100000000);
Eu tenho o plano mostrado na Figura 5 para esta execução.
Figura 5:planejar a função dbo.GetNums_AdamMachanic1 O plano é muito semelhante ao plano que você viu anteriormente para a primeira solução da Kamil, e o mesmo se aplica ao seu desempenho. Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =36687 ms, tempo decorrido =36952 ms .
E, claro, não foram necessárias leituras lógicas.
Vamos testar a função com ordem, usando a técnica de atribuição de variáveis:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_AdamMachanic1(1, 100000000) ORDER BY n;
Eu tenho o plano mostrado na Figura 6 para esta execução.
Figura 6:Planeje a função dbo.GetNums_AdamMachanic1 com ORDER BY Novamente, o plano é semelhante ao que você viu anteriormente para a primeira solução de Kamil. Não houve necessidade de classificação explícita, pois a função foi criada com a cláusula ORDER, mas o plano inclui algum trabalho para verificar se as linhas são realmente retornadas ordenadas conforme prometido.
Eu tenho as seguintes estatísticas de tempo para esta execução:
Tempo de CPU =55047 ms, tempo decorrido =55498 ms .
Em sua segunda solução, Adam também combinou uma parte CLR e uma parte T-SQL. Aqui está a descrição de Adam da lógica que ele usou em sua solução:
“Eu estava tentando pensar em como contornar o problema de conversação do SQLCLR e também o desafio central desse gerador de números em T-SQL, que é o fato de que não podemos simplesmente criar linhas mágicas.
O CLR é uma boa resposta para a segunda parte, mas é obviamente prejudicado pela primeira questão. Então, como compromisso, criei um T-SQL TVF [chamado GetNums_AdamMachanic2_8192] codificado com os valores de 1 a 8192. (Escolha bastante arbitrária, mas muito grande e o QO começa a engasgar um pouco.) Em seguida, modifiquei minha função CLR [ chamado GetNums_AdamMachanic2_8192_base] para gerar duas colunas, "max_base" e "base_add", e gerar linhas como:
- max_base, base_add
——————
8191, 1
8192, 8192
8192, 16384
…
8192, 99991552
257, 99999744
Agora é um loop simples. A saída CLR é enviada para o T-SQL TVF, que é configurado para retornar apenas as linhas "max_base" de seu conjunto codificado. E para cada linha, adiciona "base_add" ao valor, gerando assim os números necessários. A chave aqui, eu acho, é que podemos gerar N linhas com apenas uma única junção lógica cruzada, e a função CLR só precisa retornar 1/8192 do número de linhas, então é rápido o suficiente para atuar como gerador de base.”
A lógica parece bem simples.
Aqui está o código usado para definir a função CLR chamada GetNums_AdamMachanic2_8192_base:
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsAdam2
{
private struct row
{
public long max_base;
public long base_add;
}
[Microsoft.SqlServer.Server.SqlFunction(
FillRowMethodName = "GetNums_AdamMachanic2_8192_base_fill",
TableDefinition = "max_base int, base_add int")]
public static IEnumerable GetNums_AdamMachanic2_8192_base(SqlInt64 min, SqlInt64 max)
{
var min_int = min.Value;
var max_int = max.Value;
var min_group = min_int / 8192;
var max_group = max_int / 8192;
for (; min_group <= max_group; min_group++)
{
if (min_int > max_int)
yield break;
var max_base = 8192 - (min_int % 8192);
if (min_group == max_group && max_int < (((max_int / 8192) + 1) * 8192) - 1)
max_base = max_int - min_int + 1;
yield return (
new row()
{
max_base = max_base,
base_add = min_int
}
);
min_int = (min_group + 1) * 8192;
}
}
public static void GetNums_AdamMachanic2_8192_base_fill(object o, out long max_base, out long base_add)
{
var r = (row)o;
max_base = r.max_base;
base_add = r.base_add;
}
}; Eu nomeei o projeto VS GetNumsAdam2 e coloquei no caminho C:\Temp\ como nos outros projetos. Aqui está o código que usei para implantar a função no banco de dados testdb:
-- Create assembly and function DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base; DROP ASSEMBLY IF EXISTS GetNumsAdam2; GO CREATE ASSEMBLY GetNumsAdam2 FROM 'C:\Temp\GetNumsAdam2\GetNumsAdam2\bin\Debug\GetNumsAdam2.dll'; GO CREATE FUNCTION dbo.GetNums_AdamMachanic2_8192_base(@max_base AS BIGINT, @add_base AS BIGINT) RETURNS TABLE(max_base BIGINT, base_add BIGINT) ORDER(base_add) AS EXTERNAL NAME GetNumsAdam2.GetNumsAdam2.GetNums_AdamMachanic2_8192_base; GO
Aqui está um exemplo para usar GetNums_AdamMachanic2_8192_base com o intervalo de 1 a 100M:
SELECT * FROM dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);
Este código gera a seguinte saída, mostrada aqui de forma abreviada:
max_base base_add -------------------- -------------------- 8191 1 8192 8192 8192 16384 8192 24576 8192 32768 ... 8192 99966976 8192 99975168 8192 99983360 8192 99991552 257 99999744 (12208 rows affected)
Aqui está o código com a definição da função T-SQL GetNums_AdamMachanic2_8192 (abreviada):
CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT)
RETURNS TABLE
AS
RETURN
SELECT TOP (@max_base) V.i + @add_base AS val
FROM (
VALUES
(0),
(1),
(2),
(3),
(4),
...
(8187),
(8188),
(8189),
(8190),
(8191)
) AS V(i);
GO Importante: Também aqui, devo enfatizar que, semelhante ao que disse sobre a segunda solução de Kamil, Adam supõe aqui que o filtro TOP extrairá as linhas superiores com base na ordem de aparência das linhas no construtor de valor de tabela, o que não é realmente garantido. Se você adicionar uma cláusula ORDER BY para dar suporte a TOP ou alterar o filtro para um filtro WHERE, obterá um filtro determinístico, mas isso pode alterar completamente o perfil de desempenho da solução.
Finalmente, aqui está a função T-SQL mais externa, dbo.GetNums_AdamMachanic2, que o usuário final chama para obter a série numérica:
CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
SELECT Y.val AS n
FROM ( SELECT max_base, base_add
FROM dbo.GetNums_AdamMachanic2_8192_base(@low, @high) ) AS X
CROSS APPLY dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) AS Y
GO Essa função usa o operador CROSS APPLY para aplicar a função T-SQL interna dbo.GetNums_AdamMachanic2_8192 por linha retornada pela função CLR interna dbo.GetNums_AdamMachanic2_8192_base.
Vamos primeiro testar esta solução usando a técnica de agregação quando a ordem não importa:
SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic2(1, 100000000);
Eu tenho o plano mostrado na Figura 7 para esta execução.
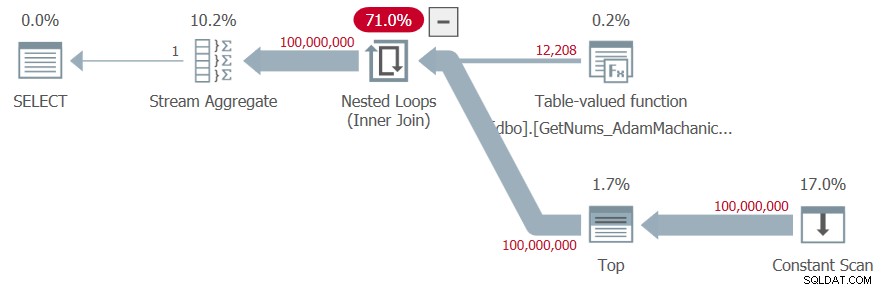Figura 7:planejar a função dbo.GetNums_AdamMachanic2 Eu obtive as seguintes estatísticas de tempo para este teste:
SQL Server tempo de análise e compilação :tempo de CPU =313 ms, tempo decorrido =339 ms .
SQL Server tempo de execução :tempo de CPU =8859 ms, tempo decorrido =8849 ms .
Nenhuma leitura lógica foi necessária.
O tempo de execução não é ruim, mas observe o alto tempo de compilação devido ao grande construtor de valor de tabela usado. Você pagaria um tempo de compilação tão alto, independentemente do tamanho do intervalo solicitado, portanto, isso é especialmente complicado ao usar a função com intervalos muito pequenos. E esta solução ainda é mais lenta que as T-SQL.
Vamos testar a função com ordem:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_AdamMachanic2(1, 100000000) ORDER BY n;
Eu tenho o plano mostrado na Figura 8 para esta execução.
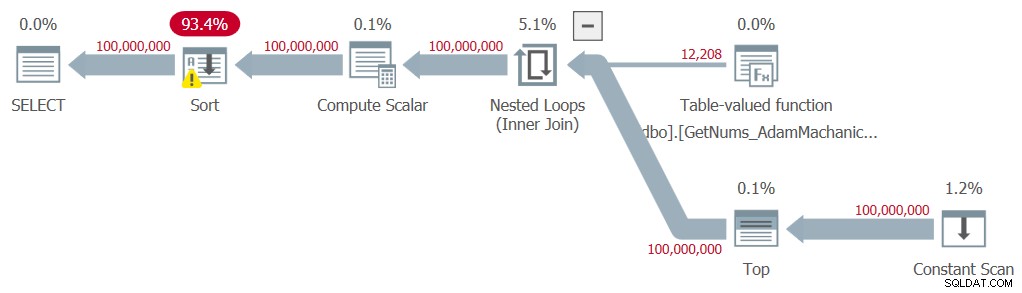Figura 8:Planeje a função dbo.GetNums_AdamMachanic2 com ORDER BY Assim como na segunda solução de Kamil, uma classificação explícita é necessária no plano, causando uma penalidade de desempenho significativa. Aqui estão as estatísticas de tempo que obtive para este teste:
Tempo de execução:tempo de CPU =54891 ms, tempo decorrido =60981 ms .
Além disso, ainda há a alta penalidade de tempo de compilação de cerca de um terço de segundo.
Conclusão
Foi interessante testar soluções baseadas em CLR para o desafio da série numérica porque muitas pessoas inicialmente presumiram que a solução com melhor desempenho provavelmente seria baseada em CLR. Kamil e Adam usaram abordagens semelhantes, com a primeira tentativa usando um loop simples que incrementa um contador e gera uma linha com o próximo valor por iteração e a segunda tentativa mais sofisticada que combina partes CLR e T-SQL. Pessoalmente, não me sinto confortável com o fato de que nas segundas soluções de Kamil e Adam eles confiaram em um filtro TOP não determinístico e, quando o converti para um determinístico em meus próprios testes, isso teve um impacto adverso no desempenho da solução . De qualquer forma, nossas duas soluções T-SQL têm um desempenho melhor do que as CLR e não resultam em classificação explícita no plano quando você precisa das linhas ordenadas. Então, eu realmente não vejo o valor em seguir a rota CLR. A Figura 9 tem um resumo de desempenho das soluções que apresentei neste artigo.
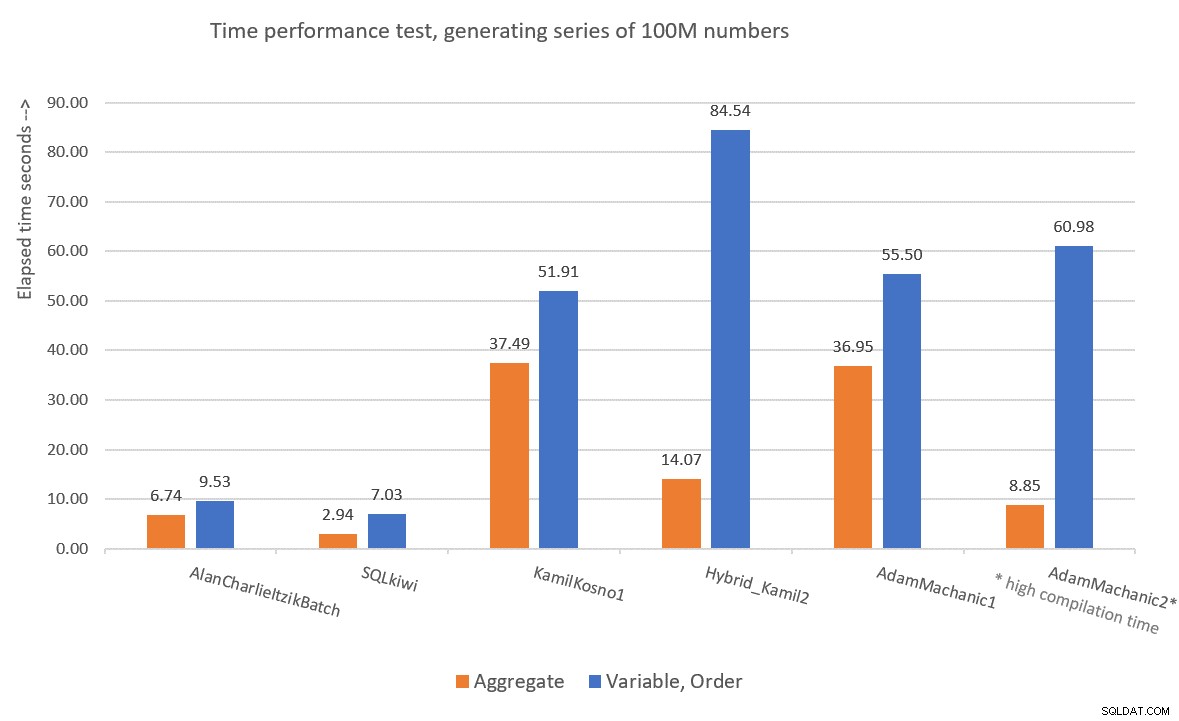Figure 9:Time performance comparison To me, GetNums_AlanCharlieItzikBatch should be the solution of choice when you require absolutely no I/O footprint, and GetNums_SQKWiki should be preferred when you don’t mind a small I/O footprint. Of course, we can always hope that one day Microsoft will add this critically useful tool as a built-in one, and hopefully if/when they do, it will be a performant solution that supports batch processing and parallelism. So don’t forget to vote for this feature improvement request, and maybe even add your comments for why it’s important for you.
I really enjoyed working on this series. I learned a lot during the process, and hope that you did too.
