No mês passado, abordei o quebra-cabeça de Peter Larsson de combinar oferta com demanda. Mostrei a solução direta baseada em cursor de Peter e expliquei que ela tem escala linear. O desafio que deixei para você é tentar encontrar uma solução baseada em um conjunto para a tarefa, e cara, as pessoas aceitaram o desafio! Obrigado Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie e, claro, Peter Larsson, por enviar suas soluções. Algumas das ideias eram brilhantes e absolutamente alucinantes.
Este mês, vou começar a explorar as soluções apresentadas, grosso modo, indo das de pior desempenho para as de melhor desempenho. Por que se preocupar com os de mau desempenho? Porque você ainda pode aprender muito com eles; por exemplo, identificando antipadrões. De fato, a primeira tentativa de resolver esse desafio para muitas pessoas, incluindo eu e Peter, é baseada em um conceito de interseção de intervalo. Acontece que a técnica clássica baseada em predicados para identificar a interseção de intervalos tem um desempenho ruim, pois não há um bom esquema de indexação para suportá-la. Este artigo é dedicado a essa abordagem de baixo desempenho. Apesar do fraco desempenho, trabalhar na solução é um exercício interessante. Requer praticar a habilidade de modelar o problema de uma maneira que se preste ao tratamento baseado em conjuntos. Também é interessante identificar o motivo do mau desempenho, tornando mais fácil evitar o antipadrão no futuro. Tenha em mente que esta solução é apenas o ponto de partida.
DDL e um pequeno conjunto de dados de amostra
Como lembrete, a tarefa envolve consultar uma tabela chamada "Leilões". Use o código a seguir para criar a tabela e preenchê-la com um pequeno conjunto de dados de exemplo:
DROP TABLE SE EXISTE dbo.Leilões; CREATE TABLE dbo.Leilões( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Leilões PRIMARY KEY CLUSTERED, Código CHAR(1) NOT NULL CONSTRAINT ck_Leilões_Code CHECK (Código ='D' OU Código ='S'), Quantidade DECIMAL(19) , 6) CONSTRAINT NOT NULL ck_Leilões_Quantidade CHECK (Quantidade> 0)); DEFINIR NOCOUNT ON; DELETE DE dbo.Leilões; SET IDENTITY_INSERT dbo.Leilões ON; INSERT INTO dbo.Leilões(ID, Código, Quantidade) VALORES (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2,0); SET IDENTITY_INSERT dbo.Leilões OFF;
Sua tarefa era criar pares que correspondam às entradas de oferta e demanda com base na ordenação de ID, gravando-as em uma tabela temporária. A seguir está o resultado desejado para o pequeno conjunto de dados de amostra:
DemandID SupplyID TradeQuantity---------- ----------- --------------1 1000 5,0000002 1000 3,0000003 2000 6,0000003 3000 2,0000005 4000 2,0000006 5000 4,0000006 6000 3,0000006 7000 1,0000007 7000 1,000000
No mês passado, também forneci um código que você pode usar para preencher a tabela Leilões com um grande conjunto de dados de amostra, controlando o número de entradas de oferta e demanda, bem como seu intervalo de quantidades. Certifique-se de usar o código do artigo do mês passado para verificar o desempenho das soluções.
Modelando os dados como intervalos
Uma ideia intrigante que se presta ao suporte de soluções baseadas em conjuntos é modelar os dados como intervalos. Em outras palavras, represente cada entrada de demanda e oferta como um intervalo começando com as quantidades totais correntes do mesmo tipo (demanda ou oferta) até, mas excluindo a corrente, e terminando com o total corrente incluindo a corrente, é claro com base no ID encomenda. Por exemplo, olhando para o pequeno conjunto de dados de amostra, a primeira entrada de demanda (ID 1) é para uma quantidade de 5,0 e a segunda (ID 2) é para uma quantidade de 3,0. A primeira entrada de demanda pode ser representada com o intervalo inicial:0,0, final:5,0, e a segunda com o intervalo inicial:5,0, final:8,0 e assim por diante.
Da mesma forma, a primeira entrada de oferta (ID 1000) é para uma quantidade de 8,0 e o segundo (ID 2000) é para uma quantidade de 6,0. A primeira entrada de suprimento pode ser representada com o intervalo inicial:0,0, final:8,0 e a segunda com o intervalo inicial:8,0, final:14,0 e assim por diante.
Os pares de oferta e demanda que você precisa criar são os segmentos sobrepostos dos intervalos de interseção entre os dois tipos.
Isso provavelmente é melhor compreendido com uma representação visual da modelagem baseada em intervalo dos dados e o resultado desejado, conforme mostrado na Figura 1.
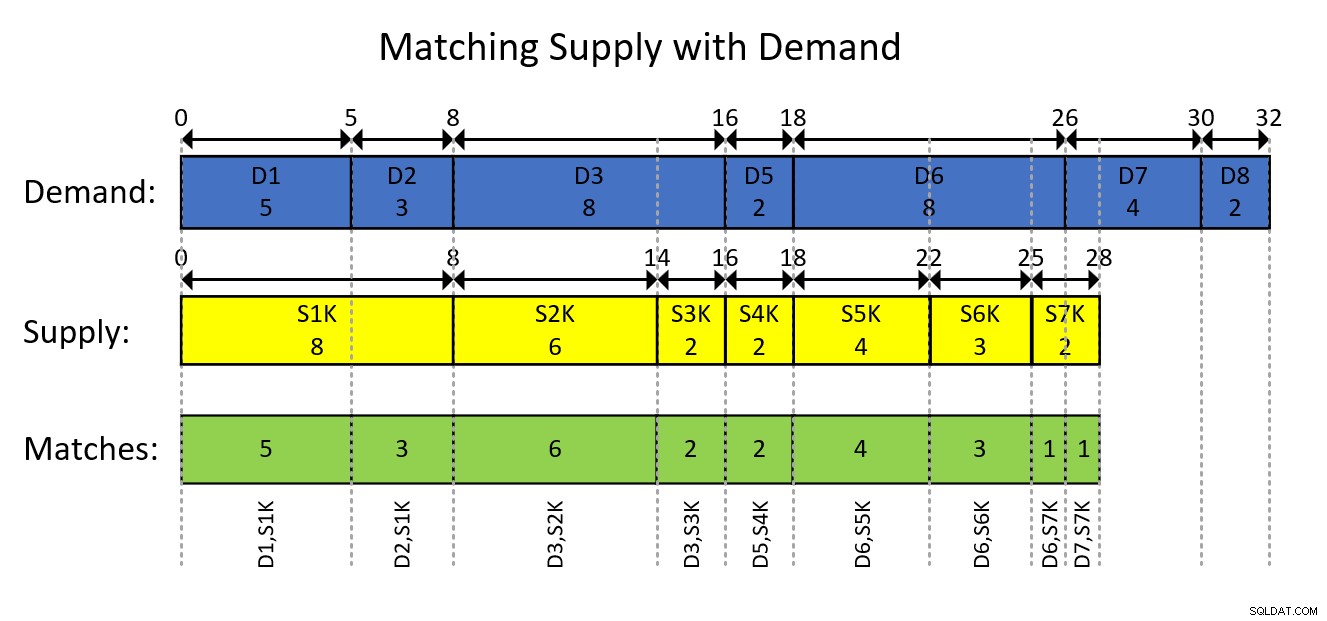 Figura 1:modelando os dados como intervalos
Figura 1:modelando os dados como intervalos A representação visual na Figura 1 é bastante autoexplicativa, mas, em resumo…
Os retângulos azuis representam as entradas de demanda como intervalos, mostrando as quantidades totais de execução exclusivas como o início do intervalo e o total de execução inclusivo como o final do intervalo. Os retângulos amarelos fazem o mesmo para entradas de suprimentos. Em seguida, observe como os segmentos sobrepostos dos intervalos de interseção dos dois tipos, representados pelos retângulos verdes, são os pares de oferta e demanda que você precisa produzir. Por exemplo, o primeiro emparelhamento de resultados é com ID de demanda 1, ID de suprimento 1000, quantidade 5. O segundo emparelhamento de resultados é com ID de demanda 2, ID de suprimento 1000, quantidade 3. E assim por diante.
Interseções de intervalo usando CTEs
Antes de começar a escrever o código T-SQL com soluções baseadas na ideia de modelagem de intervalo, você já deve ter uma noção intuitiva de quais índices provavelmente serão úteis aqui. Como você provavelmente usará funções de janela para calcular totais em execução, poderá se beneficiar de um índice de cobertura com uma chave baseada nas colunas Código, ID e incluindo a coluna Quantidade. Aqui está o código para criar esse índice:
CRIAR ÍNDICE NÃO CLUSTERADO ÚNICO idx_Code_ID_i_Quantity ON dbo.Leilões(Código, ID) INCLUDE(Quantidade);
Esse é o mesmo índice que recomendei para a solução baseada em cursor que abordei no mês passado.
Além disso, há potencial aqui para se beneficiar do processamento em lote. Você pode habilitar sua consideração sem os requisitos do modo de lote no rowstore, por exemplo, usando o SQL Server 2019 Enterprise ou posterior, criando o seguinte índice de columnstore fictício:
CRIAR ÍNDICE DE COLUMNSTORE NÃO-CLUSTERADO idx_cs ON dbo.Auctions(ID) WHERE ID =-1 AND ID =-2;
Agora você pode começar a trabalhar no código T-SQL da solução.
O código a seguir cria os intervalos que representam as entradas de demanda:
WITH D0 AS-- D0 calcula a demanda em execução como EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrai anterior EndDemand como StartDemand, expressando a demanda inicial-final como um intervaloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT *FROM D;
A consulta que define o CTE D0 filtra as entradas de demanda da tabela Leilões e calcula uma quantidade total em execução como o delimitador final dos intervalos de demanda. Em seguida, a consulta que define o segundo CTE chamado D consulta D0 e calcula o delimitador inicial dos intervalos de demanda subtraindo a quantidade atual do delimitador final.
Este código gera a seguinte saída:
ID Quantidade StartDemand EndDemand---- --------- ------------ ----------1 5,000000 0,000000 5,0000002 3,000000 5,000000 8,0000003 8,000000 8,000000 16,0000005 2,000000 16,000000 18,0000006 8,000000 18,000000 26,0000007 4,000000 26,000000 30,0000008 2,000000 30,00000
Os intervalos de abastecimento são gerados de forma muito semelhante aplicando a mesma lógica às entradas de abastecimento, usando o seguinte código:
WITH S0 AS-- S0 calcula o fornecimento em execução como EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrai anterior EndSupply como StartSupply, expressando o suprimento inicial-final como um intervaloS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT *FROM S;
Este código gera a seguinte saída:
ID Quantidade StartSupply EndSupply----- --------- ------------ ----------1000 8.000000 0.000000 8.0000002000 6.000000 8.000000 14.0000003000 2.000000 14.000000 16.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.0000006000 3.000000 22.000000 25.0000007000 2.000000 25.000000 27.000000
O que resta então é identificar os intervalos de demanda e oferta de interseção dos CTEs D e S e calcular os segmentos sobrepostos desses intervalos de interseção. Lembre-se de que os pares de resultados devem ser gravados em uma tabela temporária. Isso pode ser feito usando o seguinte código:
-- Descarta a tabela temporária se existirDROP TABLE IF EXISTS #MyPairings; WITH D0 AS-- D0 calcula a demanda em execução como EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrai anterior EndDemand como StartDemand, expressando a demanda inicial e final como um intervaloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 calcula a oferta em execução como EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER (ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Leilões WHERE Código ='S'), -- S extrai EndSupply anterior como StartSupply, expressando o suprimento inicial-final como um intervaloS AS( SELECT ID, Quantidade, EndSupply - Quantidade AS StartSupply, EndSupply FROM S0) -- A consulta externa identifica as transações como os segmentos sobrepostos dos intervalos de interseção -- Nos intervalos de interseção de demanda e oferta a quantidade de comércio é então -- MENOR(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WH EN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM D INNER JOIN S ON D.StartDemand S.StartSupply;
Além do código que cria os intervalos de demanda e oferta, que você já viu anteriormente, a principal adição aqui é a consulta externa, que identifica os intervalos de interseção entre D e S e calcula os segmentos sobrepostos. Para identificar os intervalos de interseção, a consulta externa une D e S usando o seguinte predicado de junção:
D.StartDemandS.StartSupply
Esse é o predicado clássico para identificar a interseção de intervalos. É também a principal fonte do mau desempenho da solução, como explicarei em breve.
A consulta externa também calcula a quantidade de negociação na lista SELECT como:
MENOS(EndDemand, EndSupply) - GREATEST(StartDemand, StartSupply)
Se você estiver usando o Azure SQL, poderá usar essa expressão. Se você estiver usando o SQL Server 2019 ou anterior, poderá usar a seguinte alternativa logicamente equivalente:
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END
Como o requisito era gravar o resultado em uma tabela temporária, a consulta externa usa uma instrução SELECT INTO para conseguir isso.
A ideia de modelar os dados como intervalos é claramente intrigante e elegante. Mas e o desempenho? Infelizmente, esta solução específica tem um grande problema relacionado a como a interseção de intervalo é identificada. Examine o plano para esta solução mostrada na Figura 2.
Figura 2:plano de consulta para interseções usando solução de CTEs
Vamos começar com as partes baratas do plano.
A entrada externa da junção de loops aninhados calcula os intervalos de demanda. Ele usa um operador Index Seek para recuperar as entradas de demanda e um operador Window Aggregate de modo batch para calcular o delimitador final do intervalo de demanda (referido como Expr1005 neste plano). O delimitador de início do intervalo de demanda é então Expr1005 – Quantidade (de D).
Como uma observação lateral, você pode achar o uso de um operador Sort explícito antes do operador Window Aggregate no modo de lote surpreendente aqui, uma vez que as entradas de demanda recuperadas do Index Seek já estão ordenadas por ID como a função de janela precisa que elas sejam. Isso tem a ver com o fato de que, atualmente, o SQL Server não oferece suporte a uma combinação eficiente de operação de índice de preservação de ordem paralela antes de um operador Window Aggregate de modo de lote paralelo. Se você forçar um plano serial apenas para fins de experimentação, verá o operador Sort desaparecendo. O SQL Server decidiu, em geral, o uso de paralelismo aqui foi preferido, apesar de resultar na classificação explícita adicionada. Mas, novamente, esta parte do plano representa uma pequena parte do trabalho no grande esquema das coisas.
Da mesma forma, a entrada interna da junção de loops aninhados começa calculando os intervalos de fornecimento. Curiosamente, o SQL Server optou por usar operadores de modo de linha para lidar com essa parte. Por um lado, os operadores de modo de linha usados para calcular totais em execução envolvem mais sobrecarga do que a alternativa Window Aggregate em modo de lote; por outro lado, o SQL Server tem uma implementação paralela eficiente de uma operação de índice de preservação de ordem seguida pela computação da função de janela, evitando Ordenação explícita para esta parte. É curioso que o otimizador tenha escolhido uma estratégia para os intervalos de demanda e outra para os intervalos de fornecimento. De qualquer forma, o operador Index Seek recupera as entradas de fornecimento e a seqüência subsequente de operadores até o operador Compute Scalar calcula o delimitador final do intervalo de fornecimento (referido como Expr1009 neste plano). O delimitador de início do intervalo de fornecimento é então Expr1009 – Quantidade (de S).
Apesar da quantidade de texto que usei para descrever essas duas partes, a parte realmente cara do trabalho no plano é o que vem a seguir.
A próxima parte precisa juntar os intervalos de demanda e os intervalos de fornecimento usando o seguinte predicado:
D.StartDemandS.StartSupply
Sem índice de suporte, assumindo intervalos de demanda DI e intervalos de fornecimento SI, isso envolveria o processamento de linhas DI * SI. O plano da Figura 2 foi criado após o preenchimento da tabela Leilões com 400.000 linhas (200.000 entradas de demanda e 200.000 entradas de oferta). Portanto, sem índice de suporte, o plano precisaria processar 200.000 * 200.000 =40.000.000.000 linhas. Para mitigar esse custo, o otimizador optou por criar um índice temporário (consulte o operador Index Spool) com o delimitador final do intervalo de fornecimento (Expr1009) como chave. Isso é praticamente o melhor que poderia fazer. No entanto, isso resolve apenas parte do problema. Com dois predicados de intervalo, apenas um pode ser suportado por um predicado de busca de índice. O outro deve ser tratado usando um predicado residual. De fato, você pode ver no plano que a busca no índice temporário usa o predicado de busca Expr1009> Expr1005 – D.Quantity, seguido por um operador Filter manipulando o predicado residual Expr1005> Expr1009 – S.Quantity.
Supondo que, em média, o predicado de busca isola metade das linhas de fornecimento do índice por linha de demanda, o número total de linhas emitidas pelo operador Index Spool e processadas pelo operador Filter é então DI * SI / 2. No nosso caso, com 200.000 linhas de demanda e 200.000 linhas de suprimento, isso se traduz em 20.000.000.000. De fato, a seta que vai do operador Index Spool para o operador Filter relata um número de linhas próximo a isso.
Este plano tem escala quadrática, em comparação com a escala linear da solução baseada em cursor do mês passado. Você pode ver o resultado de um teste de desempenho comparando as duas soluções na Figura 3. Você pode ver claramente a parábola bem formada para a solução baseada em conjunto.
Figura 3:Desempenho de interseções usando solução CTEs versus solução baseada em cursor
Interseções de intervalo usando tabelas temporárias
Você pode melhorar um pouco as coisas substituindo o uso de CTEs para os intervalos de demanda e fornecimento por tabelas temporárias e para evitar o spool de índice, criando seu próprio índice na tabela temporária mantendo os intervalos de fornecimento com o delimitador final como a chave. Aqui está o código da solução completa:
-- Descarta tabelas temporárias se existir DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply; WITH D0 AS-- D0 calcula a demanda em execução como EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrai anterior EndDemand como StartDemand, expressando a demanda inicial-final como um intervaloD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;WITH S0 AS-- S0 calcula o fornecimento em execução como EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Leilões WHERE Code ='S'),-- S extrai o anterior EndSupply como StartSupply, expressando o suprimento inicial-final como um intervaloS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT ID, Quantidade, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupplyINTO #SupplyFROM S; CRIAR ÍNDICE CLUSTERED ÚNICO idx_cl_ES_ID ON #Supply(EndSupply, ID); -- A consulta externa identifica as transações como os segmentos sobrepostos dos intervalos de interseção-- Nos intervalos de demanda e oferta de interseção, a quantidade de transações é então -- MENOR(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM #Demand AS D INNER JOIN #Supply AS S WITH (FORCESEEK) ON D.StartDemand S.StartSupply;
Os planos para esta solução são mostrados na Figura 4:
Figura 4:plano de consulta para interseções usando solução de tabelas temporárias
Os dois primeiros planos usam uma combinação de operadores Index Seek + Sort + Window Aggregate no modo de lote para calcular os intervalos de oferta e demanda e gravá-los em tabelas temporárias. O terceiro plano trata da criação do índice na tabela #Supply com o delimitador EndSupply como a chave principal.
O quarto plano representa de longe a maior parte do trabalho, com um operador de junção de loops aninhados que corresponde a cada intervalo de #Demand, os intervalos de interseção de #Supply. Observe que também aqui, o operador Index Seek depende do predicado #Supply.EndSupply> #Demand.StartDemand como o predicado de busca e #Demand.EndDemand> #Supply.StartSupply como o predicado residual. Portanto, em termos de complexidade/escalonamento, você obtém a mesma complexidade quadrática da solução anterior. Você apenas paga menos por linha, pois está usando seu próprio índice em vez do spool de índice usado pelo plano anterior. Você pode ver o desempenho desta solução em comparação com as duas anteriores na Figura 5.
Figura 5:Desempenho de interseções usando tabelas temporárias em comparação com outras duas soluções
Como você pode ver, a solução com as tabelas temporárias tem um desempenho melhor que a dos CTEs, mas ainda tem escala quadrática e se sai muito mal em comparação com o cursor.
O que vem a seguir?
Este artigo abordou a primeira tentativa de lidar com a tarefa clássica de correspondência entre oferta e demanda usando uma solução baseada em conjunto. A ideia era modelar os dados como intervalos, combinar a oferta com as entradas de demanda, identificando os intervalos de oferta e demanda de interseção e, em seguida, calcular a quantidade de negociação com base no tamanho dos segmentos sobrepostos. Certamente uma ideia intrigante. O principal problema com isso também é o problema clássico de identificar a interseção de intervalos usando dois predicados de intervalo. Mesmo com o melhor índice em vigor, você só pode oferecer suporte a um predicado de intervalo com uma busca de índice; o outro predicado de intervalo deve ser tratado usando um predicado residual. Isso resulta em um plano com complexidade quadrática.
Então, o que você pode fazer para superar esse obstáculo? Existem várias ideias diferentes. Uma ideia brilhante pertence a Joe Obbish, sobre a qual você pode ler em detalhes em sua postagem no blog. Abordarei outras ideias nos próximos artigos da série.
[Pular para:Desafio original | Soluções:Parte 1 | Parte 2 | Parte 3]