Database
 sql >> Base de Dados >  >> RDS >> Database

Combinando a oferta com a demanda - Soluções, Parte 2

[Pular para:Desafio original | Soluções:Parte 1 | Parte 2 | Parte 3]
Neste artigo, continuo a cobertura de soluções para o atraente desafio de oferta e demanda de Peter Larsson. Agradecemos novamente a Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie e Peter Larsson, por enviarem suas soluções.

No mês passado, abordei uma solução baseada em interseções de intervalo, usando um teste clássico de interseção de intervalo baseado em predicado. Vou me referir a essa solução como interseções clássicas . A abordagem clássica de interseções intervalares resulta em um plano com escala quadrática (N^2). Demonstrei seu baixo desempenho em relação a entradas de amostra que variam de 100K a 400K linhas. A solução levou 931 segundos para ser concluída em relação à entrada de 400 mil linhas! Este mês, começarei lembrando brevemente a solução do mês passado e por que ela escala e tem um desempenho tão ruim. Em seguida, apresentarei uma abordagem baseada em uma revisão do teste de interseção de intervalo. Essa abordagem foi usada por Luca, Kamil e possivelmente também Daniel, e permite uma solução com desempenho e escala muito melhores. Vou me referir a essa solução como interseções revisadas .

O problema com o teste de interseção clássico


Vamos começar com um lembrete rápido da solução do mês passado.

Usei os seguintes índices na tabela de entrada dbo.Auctions para dar suporte ao cálculo dos totais em execução que produzem os intervalos de demanda e oferta:
-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

O código a seguir tem a solução completa implementando a abordagem clássica de interseções de intervalo:
-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Esse código começa calculando os intervalos de demanda e oferta e gravando-os em tabelas temporárias chamadas #Demand e #Supply. O código então cria um índice clusterizado em #Supply com EndSupply como a chave principal para dar suporte ao teste de interseção da melhor maneira possível. Por fim, o código une #Supply e #Demand, identificando as negociações como os segmentos sobrepostos dos intervalos de interseção, usando o seguinte predicado de junção baseado no teste clássico de interseção de intervalos:
D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

O plano para esta solução é mostrado na Figura 1.

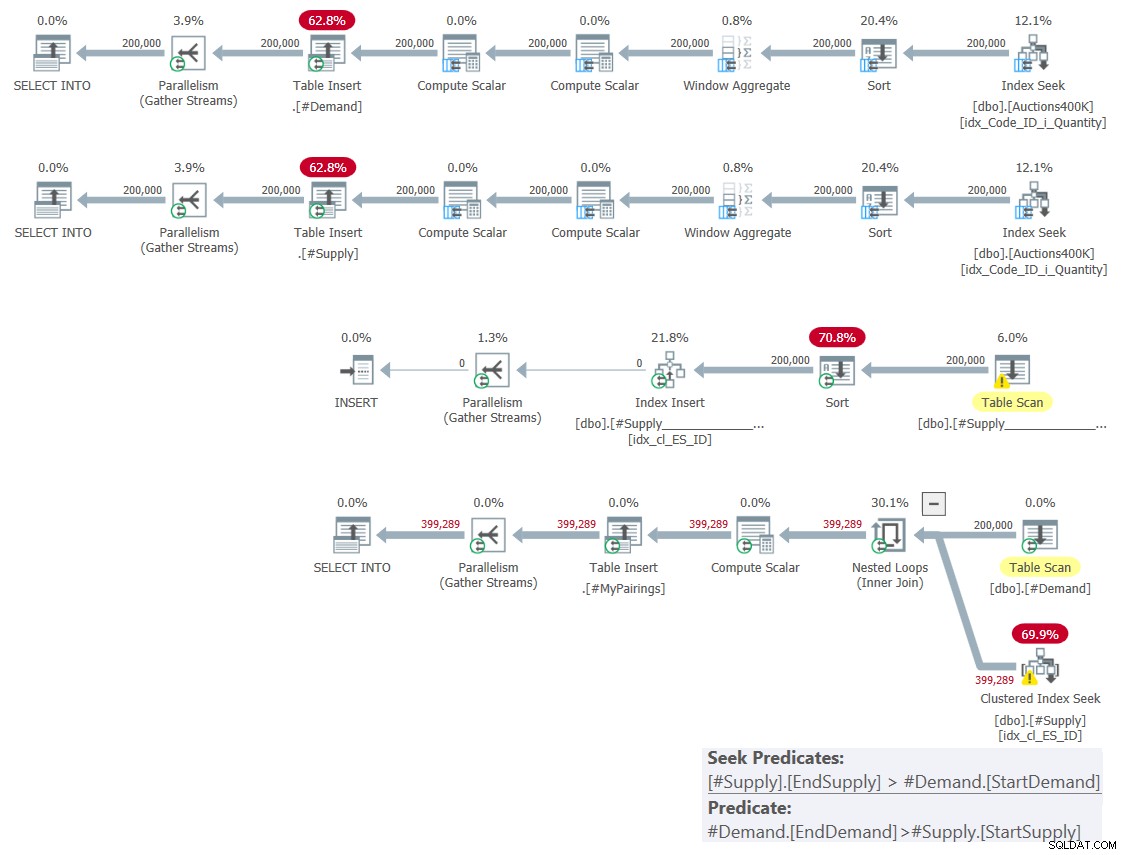Figura 1:plano de consulta para solução baseada em interseções clássicas

Como expliquei no mês passado, entre os dois predicados de intervalo envolvidos, apenas um pode ser usado como predicado de busca como parte de uma operação de busca de índice, enquanto o outro deve ser aplicado como um predicado residual. Você pode ver isso claramente no plano para a última consulta na Figura 1. É por isso que me preocupei em criar apenas um índice em uma das tabelas. Também forcei o uso de uma busca no índice que criei usando a dica FORCESEEK. Caso contrário, o otimizador pode acabar ignorando esse índice e criando um próprio usando um operador Index Spool.

Este plano tem complexidade quadrática, pois por linha em um lado—#Demanda em nosso caso—o índice de busca terá que acessar em média metade das linhas do outro lado—#Suprimento em nosso caso—com base no predicado de busca, e identificar o partidas finais aplicando o predicado residual.

Se ainda não está claro para você por que esse plano tem complexidade quadrática, talvez uma representação visual do trabalho possa ajudar, conforme mostrado na Figura 2.

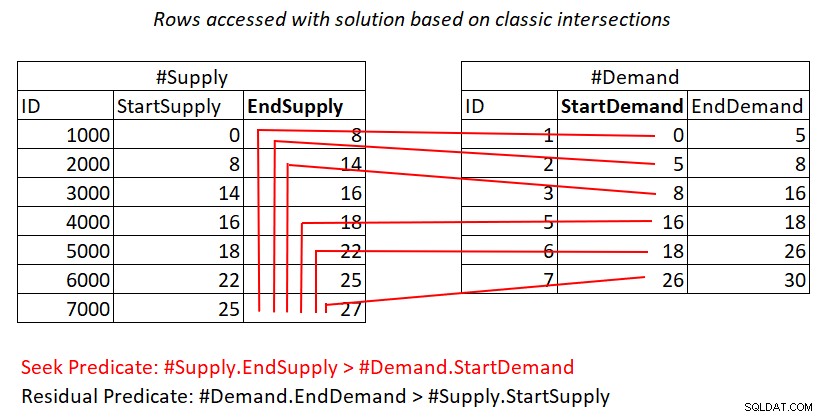Figura 2:Ilustração de trabalho com solução baseada em interseções clássicas

Esta ilustração representa o trabalho realizado pela junção de loops aninhados no plano para a última consulta. O heap #Demand é a entrada externa da junção e o índice clusterizado em #Supply (com EndSupply como a chave principal) é a entrada interna. As linhas vermelhas representam as atividades de busca de índice feitas por linha em #Demand no índice em #Supply e as linhas que elas acessam como parte das varreduras de intervalo na folha de índice. Para valores de StartDemand extremamente baixos em #Demand, a varredura de intervalo precisa acessar quase todas as linhas em #Supply. Para valores de StartDemand extremamente altos em #Demand, a varredura de intervalo precisa acessar quase zero linhas em #Supply. Em média, a varredura de intervalo precisa acessar cerca de metade das linhas em #Supply por linha em demanda. Com linhas de demanda D e linhas de fornecimento S, o número de linhas acessadas é D + D*S/2. Isso além do custo das buscas que levam você às linhas correspondentes. Por exemplo, ao preencher dbo.Auctions com 200.000 linhas de demanda e 200.000 linhas de suprimento, isso se traduz na junção de loops aninhados acessando 200.000 linhas de demanda + 200.000*200.000/2 linhas de suprimento ou 200.000 + 200.000^2/2 =20.000.200.000 linhas acessadas. Há muita redigitalização de linhas de suprimentos acontecendo aqui!

Se você deseja manter a ideia de interseções de intervalo, mas obter um bom desempenho, precisa encontrar uma maneira de reduzir a quantidade de trabalho realizado.

Em sua solução, Joe Obbish dividiu os intervalos com base no comprimento máximo do intervalo. Dessa forma, ele conseguiu reduzir o número de linhas que as junções precisavam para manipular e confiar no processamento em lote. Ele usou o teste clássico de interseção intervalar como filtro final. A solução de Joe funciona bem desde que o comprimento máximo do intervalo não seja muito alto, mas o tempo de execução da solução aumenta à medida que o comprimento máximo do intervalo aumenta.

Então o que mais você faz…?

Teste de interseção revisado


Luca, Kamil e possivelmente Daniel (havia uma parte pouco clara sobre sua solução postada devido à formatação do site, então eu tive que adivinhar) usaram um teste de interseção de intervalo revisado que permite uma utilização muito melhor da indexação.

Seu teste de interseção é uma disjunção de dois predicados (predicados separados pelo operador OR):
   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

Em inglês, o delimitador de início de demanda cruza com o intervalo de fornecimento de maneira inclusiva e exclusiva (incluindo o início e excluindo o fim); ou o delimitador de início de oferta cruza com o intervalo de demanda, de forma inclusiva e exclusiva. Para tornar os dois predicados disjuntos (não ter casos sobrepostos) mas ainda assim completos na cobertura de todos os casos, você pode manter o operador =em apenas um ou outro, por exemplo:
   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Este teste de interseção de intervalo revisado é bastante perspicaz. Cada um dos predicados pode usar um índice de forma potencialmente eficiente. Considere o predicado 1:
D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Supondo que você crie um índice de cobertura em #Demand com StartDemand como a chave principal, você pode obter uma junção de loops aninhados aplicando o trabalho ilustrado na Figura 3.


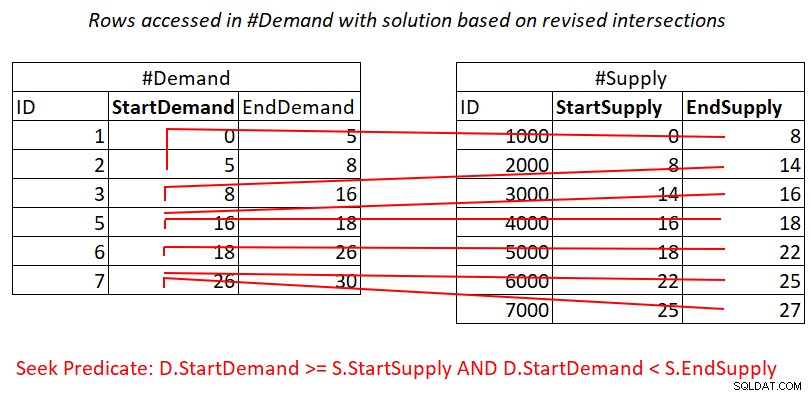
Figura 3:Ilustração do trabalho teórico necessário para processar o predicado 1

Sim, você ainda paga por uma busca no índice #Demand por linha em #Supply, mas as varreduras de intervalo na folha de índice acessam subconjuntos de linhas quase disjuntos. Sem redigitalização de linhas!

A situação é semelhante com o predicado 2:
S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Supondo que você crie um índice de cobertura em #Supply com StartSupply como a chave principal, você pode obter uma junção de loops aninhados aplicando o trabalho ilustrado na Figura 4.


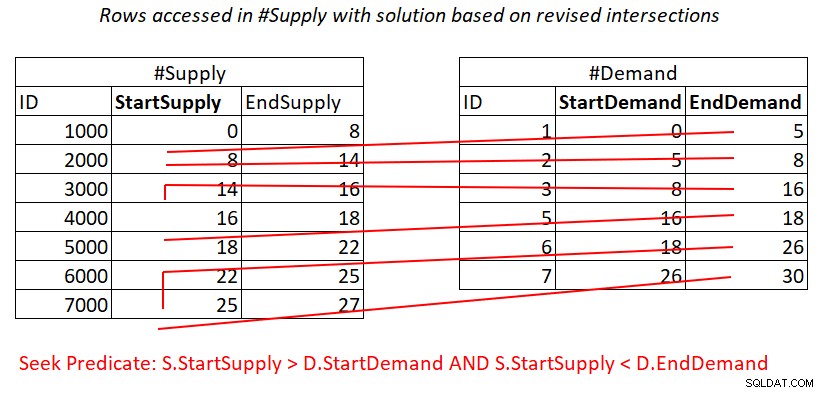
Figura 4:Ilustração do trabalho teórico necessário para processar o predicado 2

Além disso, aqui você paga por uma busca no índice #Supply por linha em #Demand e, em seguida, as varreduras de intervalo na folha de índice acessam subconjuntos quase disjuntos de linhas. Novamente, sem redigitalização de linhas!

Assumindo D linhas de demanda e S linhas de oferta, o trabalho pode ser descrito como:
Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Provavelmente, a maior parte do custo aqui é o custo de E/S envolvido com as buscas. Mas esta parte do trabalho tem escala linear em comparação com a escala quadrática da consulta clássica de interseções de intervalo.

Claro, você precisa considerar o custo preliminar da criação do índice nas tabelas temporárias, que tem escala n log n devido à classificação envolvida, mas você paga essa parte como uma parte preliminar de ambas as soluções.

Vamos tentar colocar essa teoria em prática. Vamos começar preenchendo as tabelas temporárias #Demand e #supply com os intervalos de demanda e oferta (igual às interseções de intervalo clássicas) e criando os índices de suporte:
-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

Os planos para preencher as tabelas temporárias e criar os índices são mostrados na Figura 5.


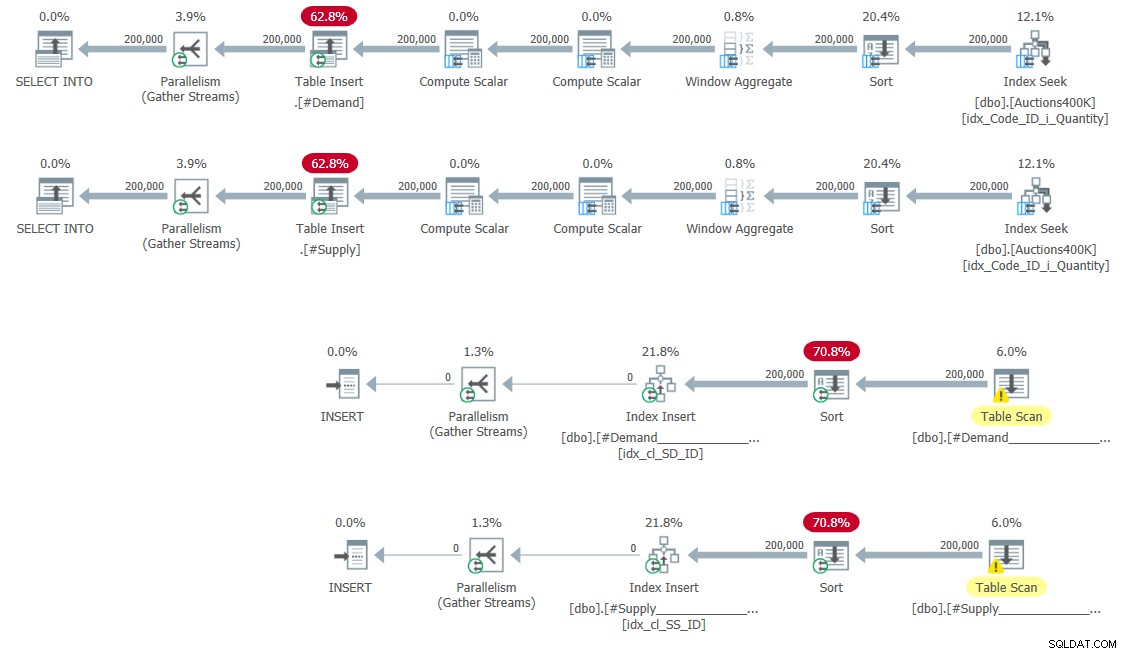
Figura 5:Planos de consulta para preencher tabelas temporárias e criar índices

Sem surpresas aqui.

Agora para a consulta final. Você pode ficar tentado a usar uma única consulta com a já mencionada disjunção de dois predicados, assim:
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

O plano para esta consulta é mostrado na Figura 6.


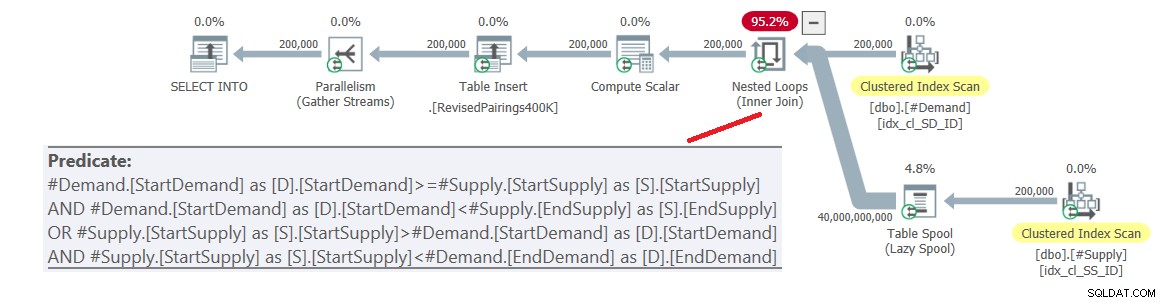
Figura 6:Plano de consulta para consulta final usando interseção revisada teste, tente 1

O problema é que o otimizador não sabe como dividir essa lógica em duas atividades separadas, cada uma lidando com um predicado diferente e utilizando o respectivo índice de forma eficiente. Assim, acaba-se com um produto cartesiano completo dos dois lados, aplicando todos os predicados como predicados residuais. Com 200.000 linhas de demanda e 200.000 linhas de suprimento, a junção processa 40.000.000.000 linhas.

O truque perspicaz usado por Luca, Kamil e possivelmente Daniel foi quebrar a lógica em duas consultas, unificando seus resultados. É aí que usar dois predicados disjuntos se torna importante! Você pode usar um operador UNION ALL em vez de UNION, evitando o custo desnecessário de procurar duplicatas. Aqui está a consulta que implementa essa abordagem:
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

O plano para esta consulta é mostrado na Figura 7.


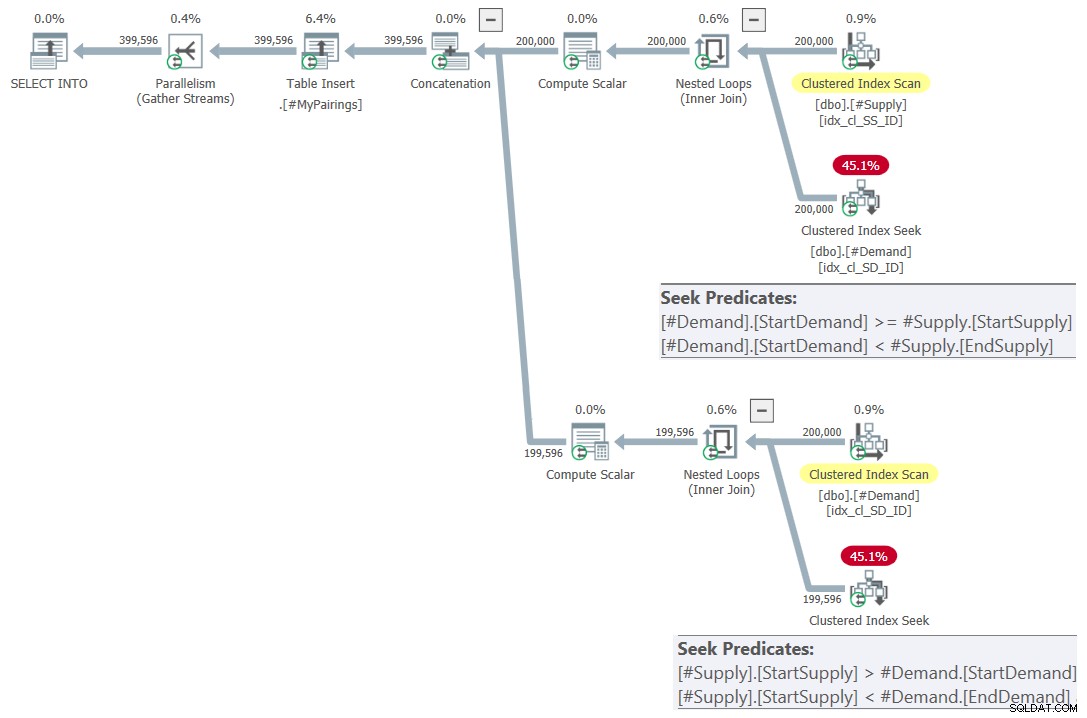
Figura 7:Plano de consulta para consulta final usando interseção revisada teste, tente 2

Isso é simplesmente lindo! Não é? E porque é tão bonito, aqui está toda a solução do zero, incluindo a criação de tabelas temporárias, indexação e a consulta final:
-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Como mencionado anteriormente, vou me referir a essa solução como interseções revisadas .

Solução de Kamil


Entre as soluções de Luca, Kamil e Daniel, a de Kamil foi a mais rápida. Aqui está a solução completa da Kamil:
SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Como você pode ver, está muito próximo da solução de interseções revisada que abordei.

O plano para a consulta final na solução da Kamil é mostrado na Figura 8.


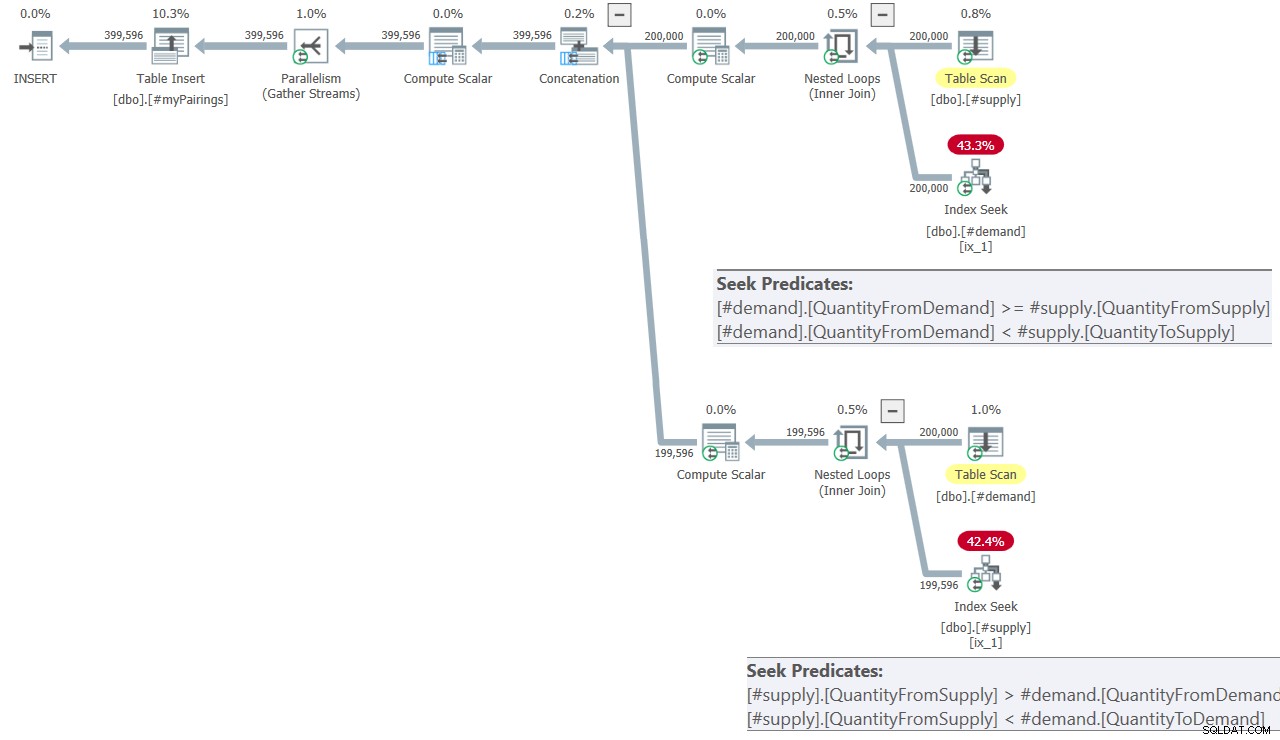
Figura 8:Plano de consulta para consulta final na solução da Kamil

O plano é bastante semelhante ao mostrado anteriormente na Figura 7.

Teste de desempenho


Lembre-se de que a solução clássica de interseções levou 931 segundos para ser concluída em uma entrada com 400 mil linhas. São 15 minutos! É muito, muito pior do que a solução do cursor, que levou cerca de 12 segundos para ser concluída com a mesma entrada. A Figura 9 apresenta os números de desempenho, incluindo as novas soluções discutidas neste artigo.


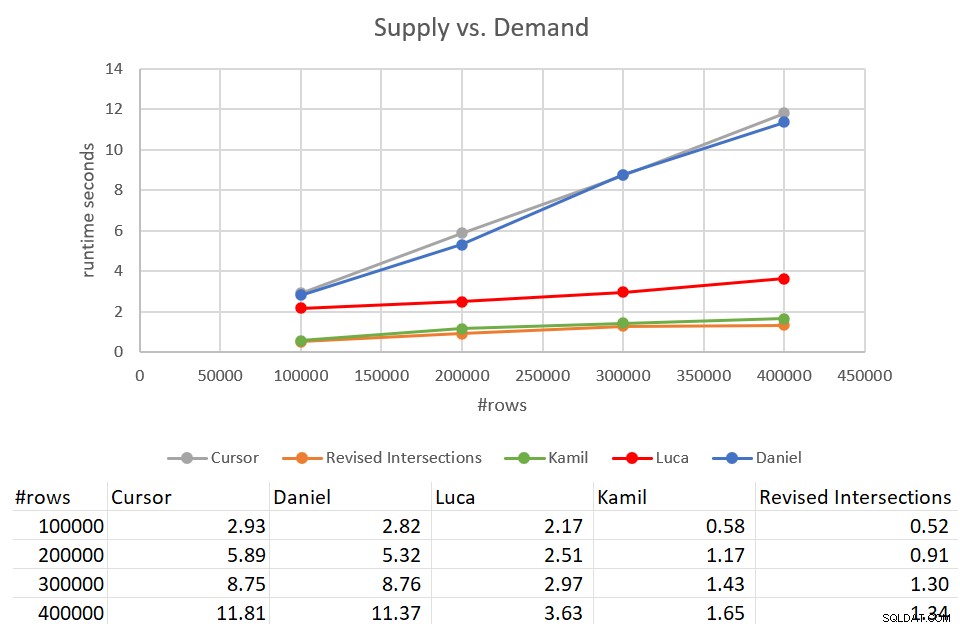
Figura 9:Teste de desempenho

Como você pode ver, a solução de Kamil e a solução de interseções revisada semelhante levou cerca de 1,5 segundo para ser concluída em relação à entrada de 400 mil linhas. Essa é uma melhoria bastante decente em comparação com a solução original baseada em cursor. A principal desvantagem dessas soluções é o custo de E/S. Com uma busca por linha, para uma entrada de 400 mil linhas, essas soluções executam um excesso de 1,35 milhão de leituras. Mas também pode ser considerado um custo perfeitamente aceitável, dado o bom tempo de execução e a escala que você obtém.

O que vem a seguir?


Nossa primeira tentativa de resolver o desafio de oferta versus demanda de correspondência baseou-se no teste clássico de interseção de intervalo e obteve um plano de baixo desempenho com escala quadrática. Muito pior do que a solução baseada em cursor. Com base nos insights de Luca, Kamil e Daniel, usando um teste de interseção de intervalo revisado, nossa segunda tentativa foi uma melhoria significativa que utiliza a indexação com eficiência e tem um desempenho melhor do que a solução baseada em cursor. No entanto, esta solução envolve um custo de E/S significativo. No próximo mês, continuarei explorando soluções adicionais.
[Pular para:Desafio original | Soluções:Parte 1 | Parte 2 | Parte 3]