Quando o SQL Server otimiza uma consulta, durante uma fase de exploração ele produz planos candidatos e escolhe entre eles aquele que tem o menor custo. O plano escolhido deve ter o menor tempo de execução entre os planos explorados. O problema é que o otimizador só pode escolher entre as estratégias que foram codificadas nele. Por exemplo, ao otimizar o agrupamento e a agregação, na data desta redação, o otimizador só pode escolher entre as estratégias Stream Aggregate e Hash Aggregate. Abordei as estratégias disponíveis nas partes anteriores desta série. Na Parte 1, abordei a estratégia Stream Aggregate pré-ordenada, na Parte 2, a estratégia Sort + Stream Aggregate, na Parte 3, a estratégia Hash Aggregate e, na Parte 4, considerações de paralelismo.
O que o otimizador do SQL Server atualmente não suporta é personalização e inteligência artificial. Ou seja, se você pode descobrir uma estratégia que sob certas condições é mais ideal do que aquelas que o otimizador suporta, você não pode aprimorar o otimizador para suportá-la e o otimizador não pode aprender a usá-la. No entanto, o que você pode fazer é reescrever a consulta usando elementos de consulta alternativos que podem ser otimizados com a estratégia que você tem em mente. Nesta quinta e última parte da série, demonstro essa técnica de ajuste de consulta usando revisões de consulta.
Muito obrigado a Paul White (@SQL_Kiwi) por ajudar com alguns dos cálculos de custos apresentados neste artigo!
Como nas partes anteriores da série, usarei o banco de dados de exemplo PerformanceV3. Use o código a seguir para descartar índices desnecessários da tabela Pedidos:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
Estratégia de otimização padrão
Considere as seguintes tarefas básicas de agrupamento e agregação:
Retorna a data máxima do pedido para cada remetente, funcionário e cliente.
Para um desempenho ideal, você cria os seguintes índices de suporte:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate); CREATE INDEX idx_eid_od ON dbo.Orders(empid, orderdate); CREATE INDEX idx_cid_od ON dbo.Orders(custid, orderdate);
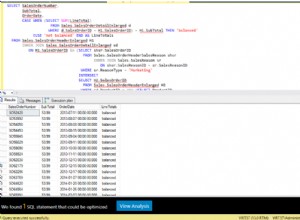
A seguir estão as três consultas que você usaria para lidar com essas tarefas, juntamente com os custos estimados da subárvore, bem como estatísticas de E/S, CPU e tempo decorrido:
-- Query 1 -- Estimated Subtree Cost: 3.5344 -- logical reads: 2484, CPU time: 281 ms, elapsed time: 279 ms SELECT shipperid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY shipperid; -- Query 2 -- Estimated Subtree Cost: 3.62798 -- logical reads: 2610, CPU time: 250 ms, elapsed time: 283 ms SELECT empid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY empid; -- Query 3 -- Estimated Subtree Cost: 4.27624 -- logical reads: 3479, CPU time: 406 ms, elapsed time: 506 ms SELECT custid, MAX(orderdate) AS maxod FROM dbo.Orders GROUP BY custid;
A Figura 1 mostra os planos para essas consultas:
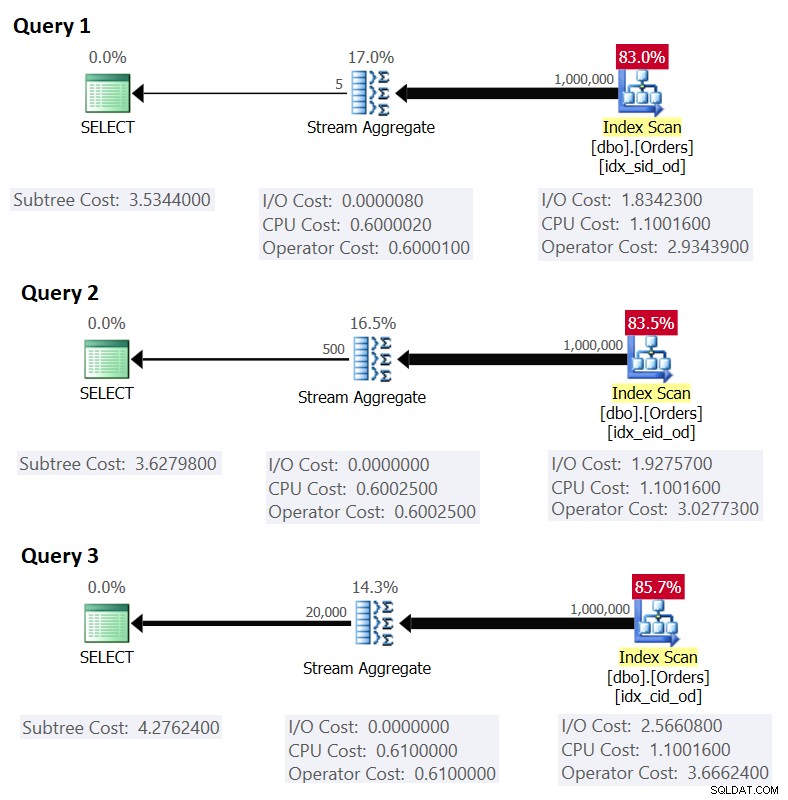Figura 1:Planos para consultas agrupadas Lembre-se de que, se você tiver um índice de cobertura em vigor, com as colunas de conjunto de agrupamento como as colunas de chave à esquerda, seguidas pela coluna de agregação, o SQL Server provavelmente escolherá um plano que execute uma verificação ordenada do índice de cobertura que dá suporte à estratégia Stream Aggregate . Como fica evidente nos planos da Figura 1, o operador Index Scan é responsável pela maior parte do custo do plano, e dentro dele a parte de E/S é a mais proeminente.
Antes de apresentar uma estratégia alternativa e explicar as circunstâncias em que ela é mais ótima do que a estratégia padrão, vamos avaliar o custo da estratégia existente. Como a parte de E/S é a mais dominante na determinação do custo do plano dessa estratégia padrão, vamos primeiro estimar quantas leituras de página lógica serão necessárias. Mais tarde, estimaremos o custo do plano também.
Para estimar o número de leituras lógicas que o operador Index Scan exigirá, você precisa saber quantas linhas você tem na tabela e quantas linhas cabem em uma página com base no tamanho da linha. Depois de ter esses dois operandos, sua fórmula para o número necessário de páginas no nível folha do índice será CEILING(1e0 * @numrows / @rowsperpage). Se tudo o que você tem é apenas a estrutura da tabela e nenhum dado de exemplo existente para trabalhar, você pode usar este artigo para estimar o número de páginas que você teria no nível folha do índice de suporte. Se você tiver bons dados de amostra representativos, mesmo que não estejam na mesma escala do ambiente de produção, poderá calcular o número médio de linhas que cabem em uma página consultando objetos de catálogo e gerenciamento dinâmico, assim:
SELECT I.name, row_count, in_row_data_page_count,
CAST(ROUND(1e0 * row_count / in_row_data_page_count, 0) AS INT) AS avgrowsperpage
FROM sys.indexes AS I
INNER JOIN sys.dm_db_partition_stats AS P
ON I.object_id = P.object_id
AND I.index_id = P.index_id
WHERE I.object_id = OBJECT_ID('dbo.Orders')
AND I.name IN ('idx_sid_od', 'idx_eid_od', 'idx_cid_od'); Essa consulta gera a seguinte saída em nosso banco de dados de exemplo:
name row_count in_row_data_page_count avgrowsperpage ----------- ---------- ---------------------- --------------- idx_sid_od 1000000 2473 404 idx_eid_od 1000000 2599 385 idx_cid_od 1000000 3461 289
Agora que você tem o número de linhas que cabem em uma página folha do índice, pode estimar o número total de páginas folha no índice com base no número de linhas que espera que sua tabela de produção tenha. Este também será o número esperado de leituras lógicas a serem aplicadas pelo operador Index Scan. Na prática, há mais no número de leituras que podem ocorrer do que apenas o número de páginas no nível folha do índice, como leituras extras produzidas pelo mecanismo de leitura antecipada, mas vou ignorá-las para manter nossa discussão simples .
Por exemplo, o número estimado de leituras lógicas para a Consulta 1 em relação ao número esperado de linhas é CEILING(1e0 * @numorws / 404). Com 1.000.000 de linhas, o número esperado de leituras lógicas é 2.476. A diferença entre 2.476 e a contagem de páginas de linha relatada de 2.473 pode ser atribuída ao arredondamento que fiz ao calcular o número médio de linhas por página.
Quanto ao custo do plano, expliquei como fazer engenharia reversa do custo do operador Stream Aggregate na Parte 1 da série. De maneira semelhante, você pode fazer engenharia reversa do custo do operador Index Scan. O custo do plano é então a soma dos custos dos operadores Index Scan e Stream Aggregate.
Para calcular o custo do operador Index Scan, você deseja começar com a engenharia reversa de algumas das importantes constantes do modelo de custo:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Com as constantes do modelo de custo acima descobertas, você pode prosseguir com a engenharia reversa das fórmulas para o custo de E/S, custo da CPU e custo total do operador para o operador Index Scan:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.003125 + (@numpages - 1e0) * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011 Operator cost: 0.002541259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000011
Por exemplo, o custo do operador Index Scan para a Consulta 1, com 2.473 páginas e 1.000.000 linhas, é:
0.002541259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000011 = 2.93439
A seguir está a fórmula de engenharia reversa para o custo do operador Stream Aggregate:
0.000008 + @numrows * 0.0000006 + @numgroups * 0.0000005
Como exemplo, para a Consulta 1, temos 1.000.000 de linhas e 5 grupos, portanto, o custo estimado é de 0,6000105.
Combinando os custos das duas operadoras, aqui está a fórmula para o custo total do plano:
0.002549259259259 + @numpages * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Para a Consulta 1, com 2.473 páginas, 1.000.000 de linhas e 5 grupos, você obtém:
0.002549259259259 + 2473 * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5344
Isso corresponde ao que a Figura 1 mostra como o custo estimado para a Consulta 1.
Se você confiasse em um número estimado de linhas por página, sua fórmula seria:
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Como exemplo, para a Consulta 1, com 1.000.000 de linhas, 404 linhas por página e 5 grupos, o custo estimado é:
0.002549259259259 + CEILING(1e0 * 1000000 / 404) * 0.000740740740741 + 1000000 * 0.0000017 + 5 * 0.0000005 = 3.5366
Como exercício, você pode aplicar os números da Consulta 2 (1.000.000 linhas, 385 linhas por página, 500 grupos) e da Consulta 3 (1.000.000 linhas, 289 linhas por página, 20.000 grupos) em nossa fórmula e ver se os resultados correspondem ao que A Figura 1 mostra.
Ajuste de consulta com regravações de consulta
A estratégia de Stream Aggregate pré-ordenada padrão para calcular um agregado MIN/MAX por grupo depende de uma varredura ordenada de um índice de cobertura de suporte (ou alguma outra atividade preliminar que emite as linhas ordenadas). Uma estratégia alternativa, com um índice de cobertura de suporte presente, seria realizar uma busca de índice por grupo. Aqui está uma descrição de um pseudo plano baseado em tal estratégia para uma consulta que agrupa por grpcol e aplica um MAX(aggcol):
set @curgrpcol = grpcol from first row obtained by a scan of the index, ordered forward;
while end of index not reached
begin
set @curagg = aggcol from row obtained by a seek to the last point
where grpcol = @curgrpcol, ordered backward;
emit row (@curgrpcol, @curagg);
set @curgrpcol = grpcol from row to the right of last row for current group;
end; Se você pensar bem, a estratégia padrão baseada em varredura é ideal quando o conjunto de agrupamento tem baixa densidade (grande número de grupos, com um pequeno número de linhas por grupo em média). A estratégia baseada em buscas é ótima quando o conjunto de agrupamento tem alta densidade (pequeno número de grupos, com grande número de linhas por grupo em média). A Figura 2 ilustra ambas as estratégias mostrando quando cada uma é ótima.
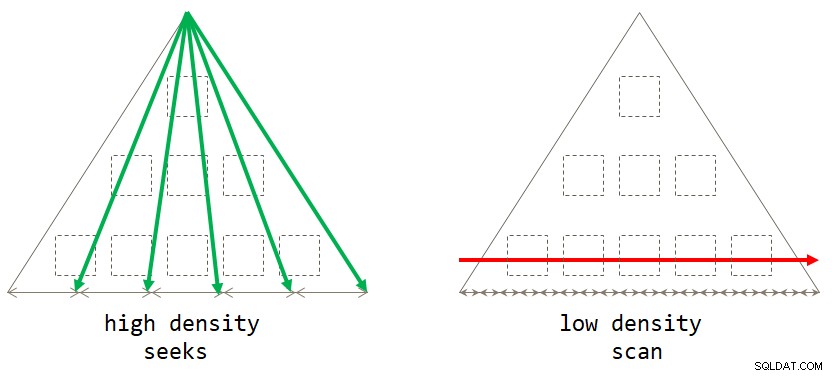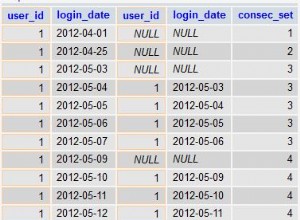
Figura 2:Estratégia ideal com base na densidade do conjunto de agrupamento Contanto que você escreva a solução na forma de uma consulta agrupada, atualmente o SQL Server considerará apenas a estratégia de verificação. Isso funcionará bem para você quando o conjunto de agrupamento tiver baixa densidade. Quando você tem alta densidade, para obter a estratégia de buscas, você precisará aplicar uma reescrita de consulta. Uma maneira de conseguir isso é consultar a tabela que contém os grupos e usar uma subconsulta de agregação escalar na tabela principal para obter a agregação. Por exemplo, para calcular a data máxima do pedido para cada remetente, você usaria o seguinte código:
SELECT shipperid,
( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS maxod
FROM dbo.Shippers AS S; As diretrizes de indexação para a tabela principal são as mesmas que suportam a estratégia padrão. Já temos esses índices para as três tarefas acima mencionadas. Você provavelmente também desejaria um índice de suporte nas colunas do conjunto de agrupamento na tabela que contém os grupos para minimizar o custo de E/S em relação a essa tabela. Use o código a seguir para criar esses índices de suporte para nossas três tarefas:
CREATE INDEX idx_sid ON dbo.Shippers(shipperid); CREATE INDEX idx_eid ON dbo.Employees(empid); CREATE INDEX idx_cid ON dbo.Customers(custid);
Um pequeno problema, porém, é que a solução baseada na subconsulta não é um equivalente lógico exato da solução baseada na consulta agrupada. Se você tiver um grupo sem presença na tabela principal, o primeiro retornará o grupo com um NULL como agregado, enquanto o último não retornará o grupo. Uma maneira simples de obter um verdadeiro equivalente lógico para a consulta agrupada é invocar a subconsulta usando o operador CROSS APPLY na cláusula FROM em vez de usar uma subconsulta escalar na cláusula SELECT. Lembre-se de que CROSS APPLY não retornará uma linha à esquerda se a consulta aplicada retornar um conjunto vazio. Aqui estão as três consultas de solução que implementam essa estratégia para nossas três tarefas, juntamente com suas estatísticas de desempenho:
-- Query 4
-- Estimated Subtree Cost: 0.0072299
-- logical reads: 2 + 15, CPU time: 0 ms, elapsed time: 43 ms
SELECT S.shipperid, A.orderdate AS maxod
FROM dbo.Shippers AS S
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.shipperid = S.shipperid
ORDER BY O.orderdate DESC ) AS A;
-- Query 5
-- Estimated Subtree Cost: 0.089694
-- logical reads: 2 + 1620, CPU time: 0 ms, elapsed time: 148 ms
SELECT E.empid, A.orderdate AS maxod
FROM dbo.Employees AS E
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.empid = E.empid
ORDER BY O.orderdate DESC ) AS A;
-- Query 6
-- Estimated Subtree Cost: 3.5227
-- logical reads: 45 + 63777, CPU time: 171 ms, elapsed time: 306 ms
SELECT C.custid, A.orderdate AS maxod
FROM dbo.Customers AS C
CROSS APPLY ( SELECT TOP (1) O.orderdate
FROM dbo.Orders AS O
WHERE O.custid = C.custid
ORDER BY O.orderdate DESC ) AS A; Os planos para essas consultas são mostrados na Figura 3.
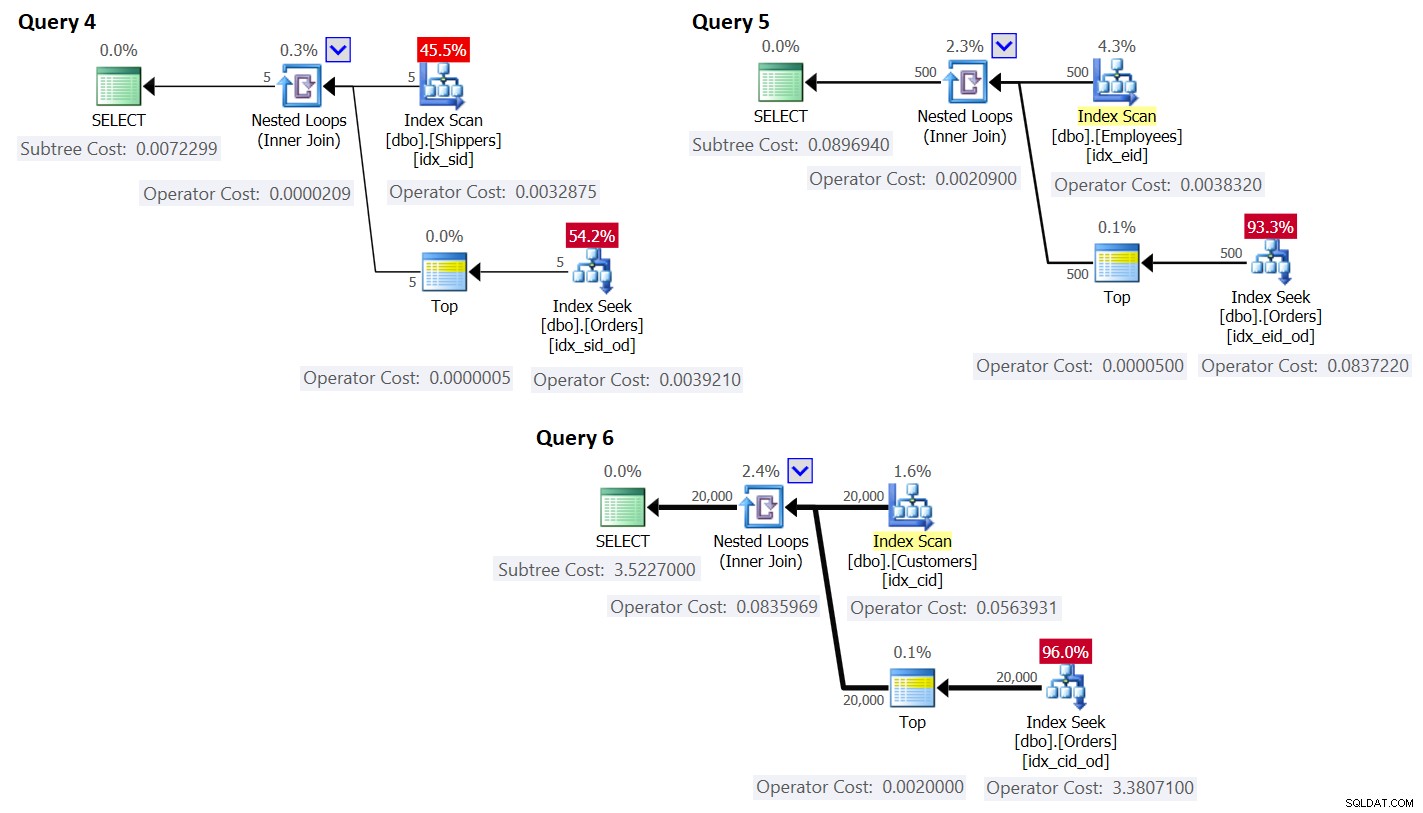Figura 3:Planos para consultas com reescrita Como você pode ver, os grupos são obtidos varrendo o índice na tabela de grupos, e o agregado é obtido aplicando uma busca no índice na tabela principal. Quanto maior a densidade do conjunto de agrupamento, mais ideal esse plano é comparado à estratégia padrão para a consulta agrupada.
Assim como fizemos anteriormente para a estratégia de varredura padrão, vamos estimar o número de leituras lógicas e planejar o custo para a estratégia de buscas. O número estimado de leituras lógicas é o número de leituras para a execução única do operador Index Scan que recupera os grupos, mais as leituras de todas as execuções do operador Index Seek.
O número estimado de leituras lógicas para o operador Index Scan é insignificante em comparação com as buscas; ainda assim, é CEILING(1e0 * @numgroups / @rowsperpage). Tome a Consulta 4 como exemplo; digamos que o índice idx_sid se encaixe em cerca de 600 linhas por página folha (o número real depende dos valores reais do shipperid, pois o tipo de dados é VARCHAR(5)). Com 5 grupos, todas as linhas cabem em uma única página de folha. Se você tivesse 5.000 grupos, eles caberiam em 9 páginas.
O número estimado de leituras lógicas para todas as execuções do operador Index Seek é @numgroups * @indexdepth. A profundidade do índice pode ser calculada como:
CEILING(LOG(CEILING(1e0 * @numrows / @rowsperleafpage), @rowspernonleafpage)) + 1
Usando a Consulta 4 como exemplo, digamos que podemos ajustar cerca de 404 linhas por página folha do índice idx_sid_od e cerca de 352 linhas por página não folha. Novamente, os números reais dependerão dos valores reais armazenados na coluna shipperid, pois seu tipo de dados é VARCHAR(5)). Para estimativas, lembre-se de que você pode usar os cálculos descritos aqui. Com bons dados de amostra representativos disponíveis, você pode usar a consulta a seguir para descobrir o número de linhas que podem caber nas páginas folha e não folha do índice fornecido:
SELECT
CASE P.index_level WHEN 0 THEN 'leaf' WHEN 1 THEN 'nonleaf' END AS pagetype,
FLOOR(8096 / (P.avg_record_size_in_bytes + 2)) AS rowsperpage
FROM (SELECT *
FROM sys.indexes
WHERE object_id = OBJECT_ID('dbo.Orders')
AND name = 'idx_sid_od') AS I
CROSS APPLY sys.dm_db_index_physical_stats
(DB_ID('PerformanceV3'), I.object_id, I.index_id, NULL, 'DETAILED') AS P
WHERE P.index_level <= 1; Obtive a seguinte saída:
pagetype rowsperpage -------- ---------------------- leaf 404 nonleaf 352
Com esses números, a profundidade do índice em relação ao número de linhas na tabela é:
CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1
Com 1.000.000 de linhas na tabela, isso resulta em uma profundidade de índice de 3. Em cerca de 50 milhões de linhas, a profundidade do índice aumenta para 4 níveis e em cerca de 17,62 bilhões de linhas aumenta para 5 níveis.
De qualquer forma, com relação ao número de grupos e número de linhas, assumindo os números acima de linhas por página, a fórmula a seguir calcula o número estimado de leituras lógicas para a Consulta 4:
CEILING(1e0 * @numgroups / 600) + @numgroups * (CEILING(LOG(CEILING(1e0 * @numrows / 404), 352)) + 1)
Por exemplo, com 5 grupos e 1.000.000 de linhas, você obtém apenas 16 leituras no total! Lembre-se de que a estratégia padrão baseada em varredura para a consulta agrupada envolve tantas leituras lógicas quanto CEILING(1e0 * @numrows / @rowsperpage). Usando a Consulta 1 como exemplo e assumindo cerca de 404 linhas por página folha do índice idx_sid_od, com o mesmo número de linhas de 1.000.000, você obtém cerca de 2.476 leituras. Aumente o número de linhas na tabela por um fator de 1.000 a 1.000.000.000, mas mantenha o número de grupos fixo. O número de leituras necessárias com a estratégia de busca muda muito pouco para 21, enquanto o número de leituras necessárias com a estratégia de varredura aumenta linearmente para 2.475.248.
A beleza da estratégia de busca é que, desde que o número de grupos seja pequeno e fixo, ela tem uma escala quase constante em relação ao número de linhas na tabela. Isso porque o número de buscas é determinado pelo número de grupos, e a profundidade do índice se relaciona com o número de linhas na tabela de forma logarítmica onde a base do log é o número de linhas que cabem em uma página não folha. Por outro lado, a estratégia baseada em varredura tem escala linear em relação ao número de linhas envolvidas.
A Figura 4 mostra o número de leituras estimado para as duas estratégias, aplicadas pela Consulta 1 e Consulta 4, dado um número fixo de grupos de 5 e diferentes números de linhas na tabela principal.
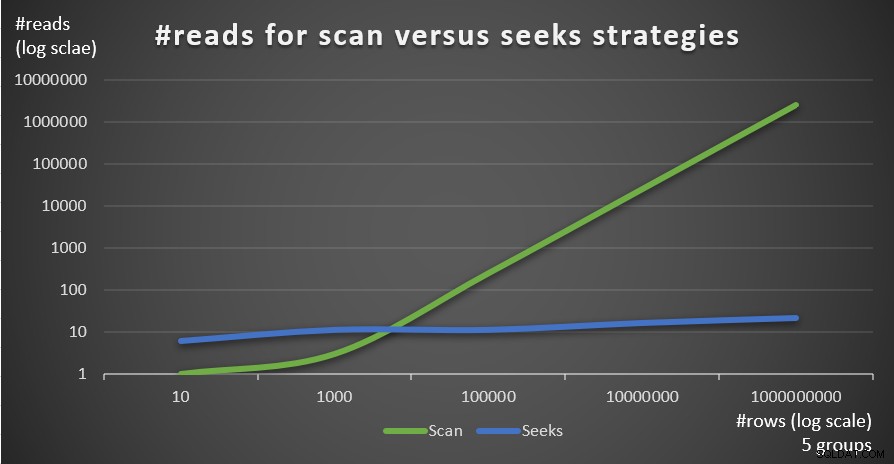Figura 4:#reads para estratégias de varredura versus busca (5 grupos) A Figura 5 mostra o número de leituras estimado para as duas estratégias, dado um número fixo de linhas de 1.000.000 na tabela principal e diferentes números de grupos.
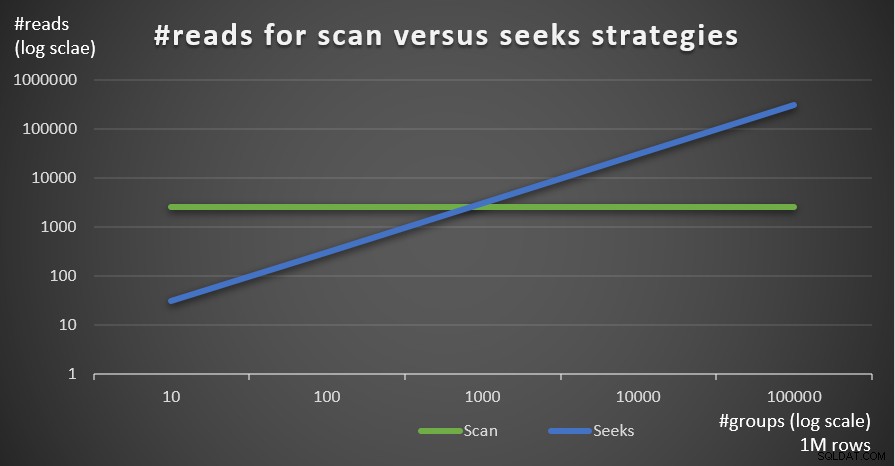Figura 5:#reads para estratégias de varredura versus busca (1 milhão de linhas) Você pode ver muito claramente que quanto maior a densidade do conjunto de agrupamento (menor número de grupos) e quanto maior a tabela principal, mais a estratégia de busca é preferida em termos de número de leituras. Se você está se perguntando sobre o padrão de E/S usado por cada estratégia; com certeza, as operações de busca de índice executam E/S aleatória, enquanto uma operação de varredura de índice executa E/S sequencial. Ainda assim, está bem claro qual estratégia é mais ideal nos casos mais extremos.
Quanto ao custo do plano de consulta, novamente, usando o plano da Consulta 4 na Figura 3 como exemplo, vamos dividi-lo para os operadores individuais no plano.
A fórmula de engenharia reversa para o custo do operador Index Scan é:
0.002541259259259 + @numpages * 0.000740740740741 + @numgroups * 0.0000011
No nosso caso, com 5 grupos, todos cabendo em uma página, o custo é:
0.002541259259259 + 1 * 0.000740740740741 + 5 * 0.0000011 = 0.0032875
O custo indicado no plano é o mesmo.
Como antes, você pode estimar o número de páginas no nível folha do índice com base no número estimado de linhas por página usando a fórmula CEILING(1e0 * @numrows / @rowsperpage), que no nosso caso é CEILING(1e0 * @ numgroups / @groupsperpage). Digamos que o índice idx_sid se encaixe em cerca de 600 linhas por página folha, com 5 grupos, você precisaria ler uma página. De qualquer forma, a fórmula de custeio para o operador Index Scan torna-se:
0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage) * 0.000740740740741 + @numgroups * 0.0000011
A fórmula de custeio de engenharia reversa para o operador de loops aninhados é:
@executions * 0.00000418
No nosso caso, isso se traduz em:
@numgroups * 0.00000418
Para a Consulta 4, com 5 grupos, você obtém:
5 * 0.00000418 = 0.0000209
O custo indicado no plano é o mesmo.
A fórmula de custeio de engenharia reversa para o operador Top é:
@executions * @toprows * 0.00000001
No nosso caso, isso se traduz em:
@numgroups * 1 * 0.00000001
Com 5 grupos, você obtém:
5 * 0.0000001 = 0.0000005
O custo indicado no plano é o mesmo.
Quanto ao operador Index Seek, aqui recebi uma grande ajuda de Paul White; obrigado, meu amigo! O cálculo é diferente para a primeira execução e para as religações (não primeiras execuções que não reutilizam o resultado da execução anterior). Como fizemos com o operador Index Scan, vamos começar identificando as constantes do modelo de custo:
@randomio = 0.003125 -- Random I/O cost @seqio = 0.000740740740741 -- Sequential I/O cost @cpubase = 0.000157 -- CPU base cost @cpurow = 0.0000011 -- CPU cost per row
Para uma execução, sem uma meta de linha aplicada, os custos de E/S e CPU são:
I/O cost: @randomio + (@numpages - 1e0) * @seqio = 0.002384259259259 + @numpages * 0.000740740740741 CPU cost: @cpubase + @numrows * @cpurow = 0.000157 + @numrows * 0.0000011
Como usamos TOP (1), temos apenas uma página e uma linha envolvidas, então os custos são:
I/O cost: 0.002384259259259 + 1 * 0.000740740740741 = 0.003125 CPU cost: 0.000157 + 1 * 0.0000011 = 0.0001581
Portanto, o custo da primeira execução do operador Index Seek no nosso caso é:
@firstexecution = 0.003125 + 0.0001581 = 0.0032831
Quanto ao custo das religações, como de costume, é feito de custos de CPU e E/S. Vamos chamá-los de @rebindcpu e @rebindio, respectivamente. Com a Consulta 4, tendo 5 grupos, temos 4 religações (chame de @rebinds). O custo @rebindcpu é a parte fácil. A fórmula é:
@rebindcpu = @rebinds * (@cpubase + @cpurow)
No nosso caso, isso se traduz em:
@rebindcpu = 4 * (0.000157 + 0.0000011) = 0.0006324
A parte do @rebindio é um pouco mais complexa. Aqui, a fórmula de custeio calcula, estatisticamente, o número esperado de páginas distintas que as reencadernações devem ler usando amostragem com reposição. Chamaremos esse elemento @pswr (para páginas distintas amostradas com substituição). A ideia é que temos @indexdatapages número de páginas no índice (no nosso caso, 2.473), e @rebinds número de religações (no nosso caso, 4). Supondo que tenhamos a mesma probabilidade de ler qualquer página com cada reencadernação, quantas páginas distintas devemos ler no total? Isso é semelhante a ter uma sacola com 2.473 bolas e quatro vezes retirar uma bola cegamente da sacola e depois devolvê-la à sacola. Estatisticamente, quantas bolas distintas você deve desenhar no total? A fórmula para isso, usando nossos operandos, é:
@pswr = @indexdatapages * (1e0 - POWER((@indexdatapages - 1e0) / @indexdatapages, @rebinds))
Com nossos números você obtém:
@pswr = 2473 * (1e0 - POWER((2473 - 1e0) / 2473, 4)) = 3.99757445099277
Em seguida, você calcula o número de linhas e páginas que você tem em média por grupo:
@grouprows = @cardinality * @density @grouppages = CEILING(@indexdatapages * @density)
Em nossa consulta 4, a cardinalidade é 1.000.000 e a densidade é 1/5 =0,2. Assim você obtém:
@grouprows = 1000000 * 0.2 = 200000 @numpages = CEILING(2473 * 0.2) = 495
Então você calcula o custo de E/S sem filtrar (chame de @io) como:
@io = @randomio + (@seqio * (@grouppages - 1e0))
No nosso caso, você obtém:
@io = 0.003125 + (0.000740740740741 * (495 - 1e0)) = 0.369050925926054
E por último, como a busca extrai apenas uma linha em cada religação, você calcula @rebindio usando a seguinte fórmula:
@rebindio = (1e0 / @grouprows) * ((@pswr - 1e0) * @io)
No nosso caso, você obtém:
@rebindio = (1e0 / 200000) * ((3.99757445099277 - 1e0) * 0.369050925926054) = 0.000005531288
Por fim, o custo do operador é:
Operator cost: @firstexecution + @rebindcpu + @rebindio = 0.0032831 + 0.0006324 + 0.000005531288 = 0.003921031288
Este é o mesmo que o custo do operador Index Seek mostrado no plano para a Consulta 4.
Agora você pode agregar os custos de todos os operadores para obter o custo completo do plano de consulta. Você obtém:
Query plan cost: 0.002541259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00000418
+ @numgroups * 0.00000001
+ 0.0032831 + (@numgroups - 1e0) * 0.0001581
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Após a simplificação, você obtém a seguinte fórmula de custeio completa para nossa estratégia Seeks:
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0))) Como exemplo, usando T-SQL, aqui está o cálculo do custo do plano de consulta com nossa estratégia Seeks para a Consulta 4:
DECLARE
@numrows AS FLOAT = 1000000,
@numgroups AS FLOAT = 5,
@rowsperpage AS FLOAT = 404,
@groupsperpage AS FLOAT = 600;
SELECT
0.005666259259259 + CEILING(1e0 * @numgroups / @groupsperpage)
* 0.000740740740741 + @numgroups * 0.0000011
+ @numgroups * 0.00016229
+ (1e0 / (@numrows / @numgroups)) * (CEILING(1e0 * @numrows / @rowsperpage)
* (1e0 - POWER((CEILING(1e0 * @numrows / @rowsperpage) - 1e0)
/ CEILING(1e0 * @numrows / @rowsperpage), @numgroups - 1e0)) - 1e0)
* (0.003125 + (0.000740740740741 * (CEILING((@numrows / @rowsperpage)
* (1e0 / @numgroups)) - 1e0)))
AS seeksplancost; Este cálculo calcula o custo 0,0072295 para a Consulta 4. O custo estimado mostrado na Figura 3 é 0,0072299. Isso é bem perto! Como exercício, calcule os custos da Consulta 5 e da Consulta 6 usando esta fórmula e verifique se você obtém números próximos aos mostrados na Figura 3.
Lembre-se de que a fórmula de custeio para a estratégia padrão baseada em varredura é (chame-a de Scan estratégia):
0.002549259259259 + CEILING(1e0 * @numrows / @rowsperpage) * 0.000740740740741 + @numrows * 0.0000017 + @numgroups * 0.0000005
Usando a Consulta 1 como exemplo e assumindo 1.000.000 de linhas na tabela, 404 linhas por página e 5 grupos, o custo estimado do plano de consulta da estratégia de varredura é 3,5366.
A Figura 6 mostra os custos estimados do plano de consulta para as duas estratégias, aplicadas pela Consulta 1 (varredura) e Consulta 4 (busca), dado um número fixo de grupos de 5 e diferentes números de linhas na tabela principal.
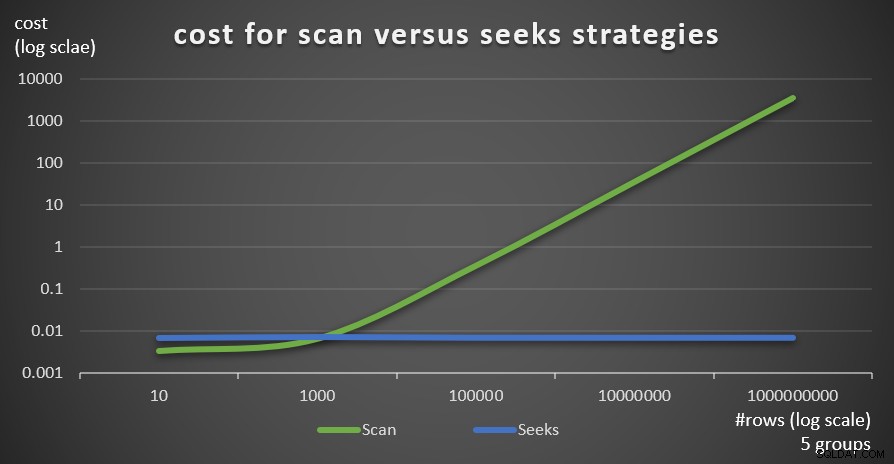Figura 6:custo para estratégias de varredura versus busca (5 grupos) A Figura 7 mostra os custos estimados do plano de consulta para as duas estratégias, dado um número fixo de linhas na tabela principal de 1.000.000 e diferentes números de grupos.
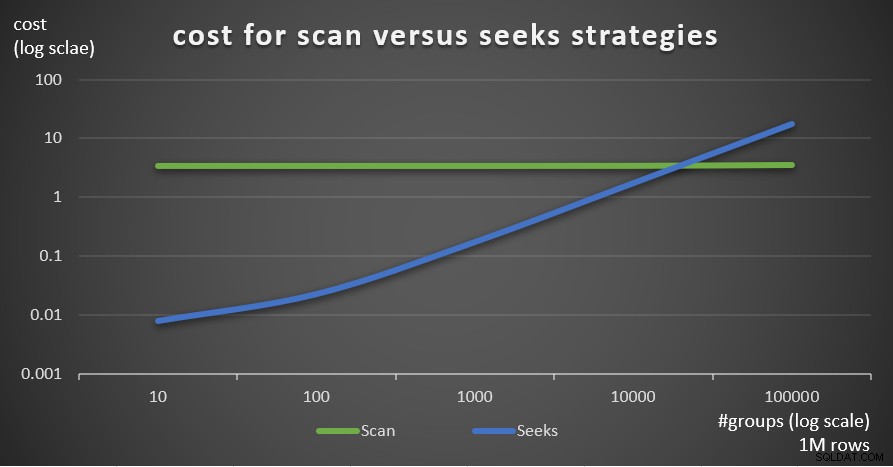Figura 7:custo para estratégias de varredura versus busca (1 milhão de linhas) Como é evidente a partir dessas descobertas, quanto maior a densidade do conjunto de agrupamento e mais linhas na tabela principal, mais ótima a estratégia de busca é comparada à estratégia de varredura. Portanto, em cenários de alta densidade, certifique-se de experimentar a solução baseada em APPLY. Enquanto isso, podemos esperar que a Microsoft adicione essa estratégia como uma opção integrada para consultas agrupadas.
Conclusão
Este artigo conclui uma série de cinco partes sobre limites de otimização de consulta para consultas que agrupam e agregam dados. Um objetivo da série foi discutir as especificidades dos vários algoritmos que o otimizador pode usar, as condições sob as quais cada algoritmo é preferido e quando você deve intervir com suas próprias reescritas de consulta. Outro objetivo foi explicar o processo de descobrir as várias opções e compará-las. Obviamente, o mesmo processo de análise pode ser aplicado à filtragem, junção, janelas e muitos outros aspectos da otimização de consultas. Espero que agora você se sinta mais equipado para lidar com o ajuste de consultas do que antes.
