Deixando de lado o WB (que não é realmente necessário para responder à sua pergunta) - o problema parece ter uma resposta direta baseada apenas em como as expressões são avaliadas durante as atribuições. Aqui está um exemplo:
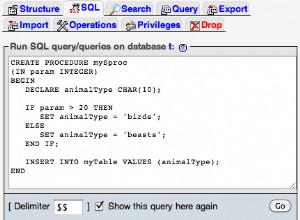
In[1505]:=
notGoodQ[x_]:=True;
Clear[g];
g[x_?notGoodQ]:=(Message[g::nogood,x];Abort[])
In[1509]:= g/:cccQ[g[x0_]]:=True
During evaluation of In[1509]:= g::nogood: -- Message text not found -- (x0_)
Out[1509]= $Aborted
Para fazê-lo funcionar, eu deliberadamente fiz uma definição para
notGoodQ para sempre retornar True . Agora, por que foi g[x0_] avaliado durante a atribuição através de TagSetDelayed ? A resposta é que, enquanto TagSetDelayed (assim como SetDelayed ) em uma atribuição h/:f[h[elem1,...,elemn]]:=... não aplica nenhuma regra que f pode ter, ele avaliará h[elem1,...,elem2] , bem como f . Aqui está um exemplo:In[1513]:=
ClearAll[h,f];
h[___]:=Print["Evaluated"];
In[1515]:= h/:f[h[1,2]]:=3
During evaluation of In[1515]:= Evaluated
During evaluation of In[1515]:= TagSetDelayed::tagnf: Tag h not found in f[Null]. >>
Out[1515]= $Failed
O fato de
TagSetDelayed é HoldAll não significa que ele não avalie seus argumentos - significa apenas que os argumentos chegam a ele sem avaliação, e se eles serão avaliados ou não depende da semântica de TagSetDelayed (que eu descrevi brevemente acima). O mesmo vale para SetDelayed , portanto, a declaração comumente usada de que "não avalia seus argumentos" não está literalmente correta. Uma afirmação mais correta é que ela recebe os argumentos não avaliados e os avalia de uma maneira especial - não avalia o r.h.s, enquanto para l.h.s. avalia cabeça e elementos, mas não aplica regras para a cabeça. Para evitar isso, você pode envolver as coisas em HoldPattern , assim:Clear[g,notGoodQ];
notGoodQ[x_]:=EvenQ[x];
g[x_?notGoodQ]:=(Message[g::nogood,x];Abort[])
g/:cccQ[HoldPattern[g[x0_]]]:=True;
Isso passa. Aqui está algum uso:
In[1527]:= cccQ[g[1]]
Out[1527]= True
In[1528]:= cccQ[g[2]]
During evaluation of In[1528]:= g::nogood: -- Message text not found -- (2)
Out[1528]= $Aborted
Observe, no entanto, que a necessidade de
HoldPattern dentro do seu lado esquerdo ao fazer uma definição geralmente é um sinal de que a expressão dentro de sua cabeça também pode ser avaliada durante a chamada de função, o que pode quebrar seu código. Aqui está um exemplo do que quero dizer:In[1532]:=
ClearAll[f,h];
f[x_]:=x^2;
f/:h[HoldPattern[f[y_]]]:=y^4;
Este código tenta capturar casos como
h[f[something]] , mas obviamente falhará, pois f[something] avaliará antes que a avaliação chegue a h :In[1535]:= h[f[5]]
Out[1535]= h[25]
Para mim, a necessidade de
HoldPattern no l.h.s. é um sinal de que preciso reconsiderar meu design. EDITAR
Com relação à depuração durante o carregamento no WB, uma coisa que você pode fazer (IIRC, não pode verificar agora) é usar as boas e velhas instruções de impressão, cuja saída aparecerá no console do WB. Pessoalmente, raramente sinto necessidade de depurador para esse fim (pacote de depuração ao carregar)
EDITAR 2
Em resposta à edição na pergunta:
Em relação à ordem das definições:sim, você pode fazer isso e resolve esse problema específico. Mas, geralmente, isso não é robusto, e eu não o consideraria um bom método geral. É difícil dar um conselho definitivo para um caso em questão, pois está um pouco fora de seu contexto, mas me parece que o uso de
UpValues aqui é injustificável. Se isso for feito para tratamento de erros, há outras maneiras
para fazer isso sem usar UpValues . Geralmente,
UpValues são usados mais comumente para sobrecarregar alguma função de forma segura, sem adicionar nenhuma regra à função que está sendo sobrecarregada. Um conselho é evitar associar UpValues com cabeças que também têm DownValues e pode avaliar - fazendo isso você começa a jogar um jogo com avaliador, e eventualmente perderá. O mais seguro é anexar UpValues a símbolos inertes (cabeças, contêineres), que geralmente representam um "tipo" de objetos nos quais você deseja sobrecarregar uma determinada função. Em relação ao meu comentário sobre a presença de
HoldPattern indicando um projeto ruim. Certamente há usos legítimos para HoldPattern , como este (um pouco artificial):In[25]:=
Clear[ff,a,b,c];
ff[HoldPattern[Plus[x__]]]:={x};
ff[a+b+c]
Out[27]= {a,b,c}
Aqui se justifica porque em muitos casos
Plus permanece não avaliado, e é útil em sua forma não avaliada - pois pode-se deduzir que ele representa uma soma. Precisamos de HoldPattern aqui por causa do modo Plus é definido em um único argumento e porque um padrão é um único argumento (mesmo que descreva geralmente vários argumentos) durante a definição. Então, usamos HoldPattern aqui para evitar tratar o padrão como argumento normal, mas isso é principalmente diferente dos casos de uso pretendidos para Plus . Sempre que esse for o caso (temos certeza de que a definição funcionará corretamente para os casos de uso pretendidos), HoldPattern está bem. Observe b.t.w., que este exemplo também é frágil:In[28]:= ff[Plus[a]]
Out[28]= ff[a]
A razão pela qual ainda está tudo bem é que normalmente não usamos
Plus em um único argumento. Mas, há um segundo grupo de casos, onde a estrutura dos argumentos normalmente fornecidos é a mesma que a estrutura dos padrões usados para a definição. Nesse caso, a avaliação do padrão durante a atribuição indica que a mesma avaliação acontecerá com os argumentos reais durante as chamadas da função. Seu uso se enquadra nesta categoria. Meu comentário para uma falha de design foi para esses casos - você pode impedir que o padrão seja avaliado, mas terá que impedir que os argumentos sejam avaliados também, para que isso funcione. E a correspondência de padrões com expressões não completamente avaliadas é frágil. Além disso, a função nunca deve assumir algumas condições extras (além do que ela pode verificar) para os argumentos.