Combinações de retorno
Usando uma tabela de números ou CTE gerador de números, selecione 0 a 2^n - 1. Usando as posições de bit contendo 1s nesses números para indicar a presença ou ausência dos membros relativos na combinação e eliminando aqueles que não têm o número correto de valores, você poderá retornar um conjunto de resultados com todas as combinações desejadas.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Essa consulta funciona muito bem, mas pensei em uma maneira de otimizá-la, usando o Contagem de bits paralela bacana para primeiro obter o número certo de itens retirados de cada vez. Isso funciona de 3 a 3,5 vezes mais rápido (tanto CPU quanto tempo):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Eu fui e li a página de contagem de bits e acho que isso poderia ter um desempenho melhor se eu não fizer o % 255, mas seguir todo o caminho com aritmética de bits. Quando tiver oportunidade vou experimentar e ver como fica.
Minhas declarações de desempenho são baseadas nas consultas executadas sem a cláusula ORDER BY. Para maior clareza, o que este código está fazendo é contar o número de bits 1 definidos em
Num dos Numbers tabela. Isso porque o número está sendo usado como uma espécie de indexador para escolher quais elementos do conjunto estão na combinação atual, então o número de 1 bits será o mesmo. Espero que você goste!
Para que conste, essa técnica de usar o padrão de bits de inteiros para selecionar membros de um conjunto é o que denominei de "União Cruzada Vertical". Isso resulta efetivamente na junção cruzada de vários conjuntos de dados, onde o número de conjuntos e junções cruzadas é arbitrário. Aqui, o número de conjuntos é o número de itens retirados de cada vez.
Na verdade, a junção cruzada no sentido horizontal usual (de adicionar mais colunas à lista existente de colunas com cada junção) seria algo assim:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Minhas consultas acima efetivamente "cross join" quantas vezes forem necessárias com apenas uma junção. Os resultados não são dinâmicos em comparação com as junções cruzadas reais, com certeza, mas isso é uma questão menor.
Crítica do seu código
Primeiro, sugiro esta mudança para sua UDF Fatorial:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Agora você pode calcular conjuntos muito maiores de combinações, além de ser mais eficiente. Você pode até considerar usar
decimal(38, 0) para permitir cálculos intermediários maiores em seus cálculos de combinação. Segundo, sua consulta não retorna os resultados corretos. Por exemplo, usando meus dados de teste do teste de desempenho abaixo, o conjunto 1 é o mesmo que o conjunto 18. Parece que sua consulta usa uma faixa deslizante que envolve:cada conjunto é sempre 5 membros adjacentes, parecido com isso (girei para facilitar a visualização):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Compare o padrão das minhas consultas:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Apenas para direcionar o padrão de bits -> índice de combinação para qualquer pessoa interessada, observe que 31 em binário =11111 e o padrão é ABCDE. 121 em binário é 1111001 e o padrão é A__DEFG (mapeado para trás).
Resultados de desempenho com uma tabela de números reais
Eu executei alguns testes de desempenho com grandes conjuntos na minha segunda consulta acima. Não tenho registro neste momento da versão do servidor utilizada. Aqui estão meus dados de teste:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter mostrou que essa "junção cruzada vertical" não funciona tão bem quanto simplesmente escrever SQL dinâmico para realmente fazer os CROSS JOINs que ela evita. Ao custo trivial de mais algumas leituras, sua solução tem métricas entre 10 e 17 vezes melhores. O desempenho de sua consulta diminui mais rápido que o meu à medida que a quantidade de trabalho aumenta, mas não rápido o suficiente para impedir que alguém o use.
O segundo conjunto de números abaixo é o fator dividido pela primeira linha da tabela, apenas para mostrar como ele é dimensionado.
Erick
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Pedro
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Extrapolando, eventualmente minha consulta será mais barata (embora seja desde o início em reads), mas não por muito tempo. Para usar 21 itens no conjunto já é necessário uma tabela de números que vai até 2097152...
Aqui está um comentário que fiz originalmente antes de perceber que minha solução teria um desempenho drasticamente melhor com uma tabela de números em tempo real:
Resultados de desempenho com uma tabela de números em tempo real
Quando escrevi originalmente esta resposta, eu disse:
Bem, eu tentei, e os resultados foram que ele teve um desempenho muito melhor! Aqui está a consulta que usei:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Observe que selecionei os valores em variáveis para reduzir o tempo e a memória necessários para testar tudo. O servidor ainda faz o mesmo trabalho. Modifiquei a versão de Peter para ser semelhante e removi extras desnecessários para que ambos fossem o mais enxutos possível. A versão do servidor usada para esses testes é
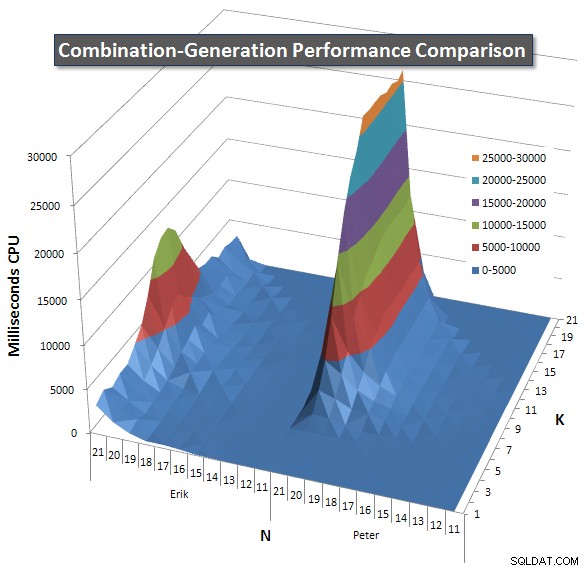
Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) rodando em uma VM. Abaixo estão os gráficos que mostram as curvas de desempenho para valores de N e K até 21. Os dados básicos para eles estão em outra resposta nesta página . Os valores são o resultado de 5 execuções de cada consulta em cada valor K e N, seguidos da eliminação dos melhores e piores valores para cada métrica e da média dos 3 restantes.
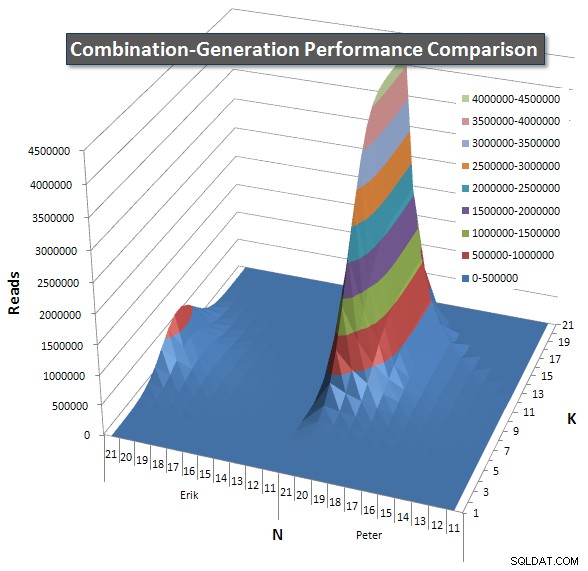
Basicamente, minha versão tem um "ombro" (no canto esquerdo do gráfico) em valores altos de N e valores baixos de K que fazem com que ela tenha um desempenho pior do que a versão SQL dinâmica. No entanto, isso permanece bastante baixo e constante, e o pico central em torno de N =21 e K =11 é muito menor para Duração, CPU e Leituras do que a versão SQL dinâmica.
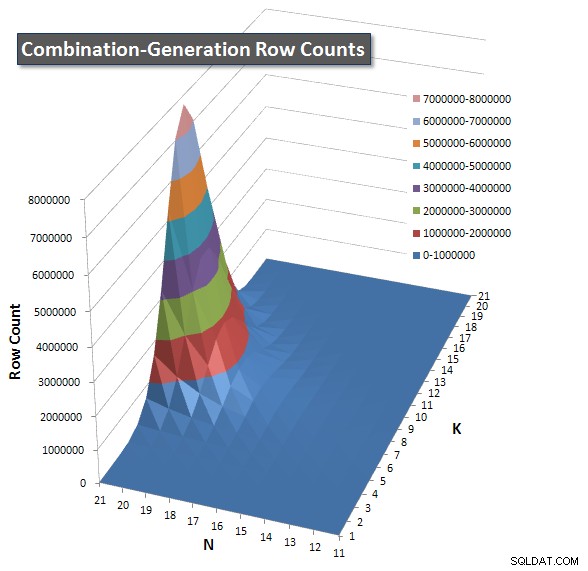
Incluí um gráfico do número de linhas que cada item deve retornar para que você possa ver o desempenho da consulta em comparação com o tamanho do trabalho que ela precisa fazer.
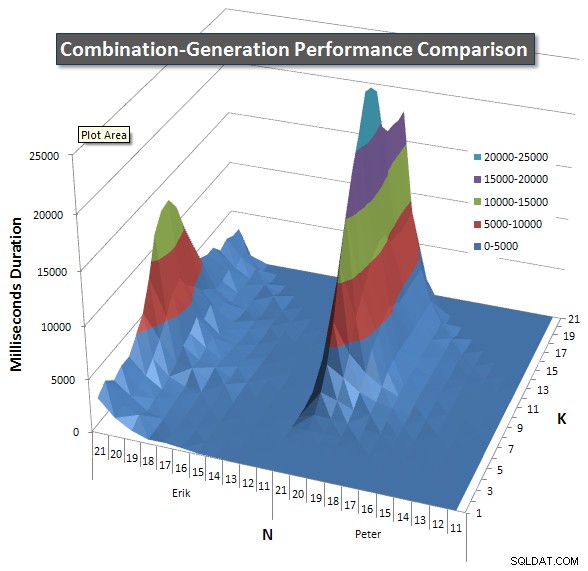
Consulte minha resposta adicional nesta página para os resultados de desempenho completos. Eu atingi o limite de caracteres do post e não consegui incluí-lo aqui. (Alguma ideia de onde mais colocá-lo?) Para colocar as coisas em perspectiva em relação aos resultados de desempenho da minha primeira versão, aqui está o mesmo formato de antes:
Erick
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Pedro
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Conclusões
- As tabelas de números em tempo real são melhores do que uma tabela real contendo linhas, já que a leitura de uma em contagens de linhas enormes requer muita E/S. É melhor usar um pouco de CPU.
- Meus testes iniciais não foram amplos o suficiente para realmente mostrar as características de desempenho das duas versões.
- A versão de Peter pode ser melhorada fazendo com que cada JOIN não seja apenas maior que o item anterior, mas também restrinja o valor máximo com base em quantos itens a mais precisam ser ajustados no conjunto. Por exemplo, em 21 itens tomados 21 por vez, há apenas uma resposta de 21 linhas (todos os 21 itens, uma vez), mas os conjuntos de linhas intermediários na versão SQL dinâmica, no início do plano de execução, contêm combinações como " AU" na etapa 2, mesmo que isso seja descartado na próxima junção, pois não há valor maior que "U" disponível. Da mesma forma, um conjunto de linhas intermediário na etapa 5 conterá "ARSTU", mas a única combinação válida neste ponto é "ABCDE". Esta versão melhorada não teria um pico mais baixo no centro, então possivelmente não o melhoraria o suficiente para se tornar o vencedor claro, mas pelo menos se tornaria simétrico para que os gráficos não ficassem no máximo além do meio da região, mas caíssem para trás para perto de 0 como minha versão faz (veja o canto superior dos picos para cada consulta).
Análise de duração
- Não há diferença realmente significativa entre as versões na duração (>100ms) até 14 itens, 12 por vez. Até este ponto, minha versão vence 30 vezes e a versão SQL dinâmica vence 43 vezes.
- A partir de 14•12, minha versão era 65 vezes mais rápida (59>100ms), a versão SQL dinâmica 64 vezes (60>100ms). No entanto, todas as vezes que minha versão foi mais rápida, economizou uma duração média total de 256,5 segundos e, quando a versão dinâmica do SQL foi mais rápida, economizou 80,2 segundos.
- A duração média total de todas as tentativas foi Erik 270,3 segundos, Peter 446,2 segundos.
- Se uma tabela de pesquisa fosse criada para determinar qual versão usar (escolhendo a mais rápida para as entradas), todos os resultados poderiam ser executados em 188,7 segundos. Usar o mais lento de cada vez levaria 527,7 segundos.
Lê análise
A análise de duração mostrou minha consulta ganhando por uma quantidade significativa, mas não excessivamente grande. Quando a métrica é alterada para leituras, surge uma imagem muito diferente - minha consulta usa em média 1/10 das leituras.
- Não há diferença realmente significativa entre as versões em leituras (>1000) até 9 itens tirados 9 de cada vez. Até este ponto, minha versão vence 30 vezes e a versão SQL dinâmica vence 17 vezes.
- A partir de 9•9, minha versão usou menos leituras 118 vezes (113>1000), a versão SQL dinâmica 69 vezes (31>1000). No entanto, todas as vezes que minha versão usou menos leituras, economizou uma média total de 75,9 milhões de leituras e, quando a versão dinâmica do SQL foi mais rápida, economizou 380 mil leituras.
- A média total de leituras para todos os testes foi Erik 8,4 milhões, Peter 84 milhões.
- Se uma tabela de pesquisa fosse criada para determinar qual versão usar (escolhendo a melhor para as entradas), todos os resultados poderiam ser executados em 8 milhões de leituras. Usar o pior de cada vez levaria 84,3 milhões de leituras.
Eu estaria muito interessado em ver os resultados de uma versão SQL dinâmica atualizada que coloca o limite superior extra nos itens escolhidos em cada etapa, conforme descrevi acima.
Adendo
A versão a seguir da minha consulta alcança uma melhoria de cerca de 2,25% em relação aos resultados de desempenho listados acima. Eu usei o método de contagem de bits HAKMEM do MIT e adicionei um
Convert(int) no resultado de row_number() uma vez que retorna um bigint. É claro que eu gostaria que esta fosse a versão que eu usei para todos os testes de desempenho, gráficos e dados acima, mas é improvável que eu a refaça, pois era trabalhoso. WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
E não resisti em mostrar mais uma versão que faz uma pesquisa para obter a contagem de bits. Pode até ser mais rápido que outras versões:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))