Estimativa de junção do SQL Server usando o alinhamento grosseiro do histograma

As principais alterações feitas na estimativa de cardinalidade a partir da versão SQL Server 2014 são descritas no white paper da Microsoft Otimizando seus planos de consulta com o estimador de cardinalidade do SQL Server 2014 por Joe Sack, Yi Fang e Vassilis Papadimos.

Uma dessas mudanças diz respeito à estimativa de junções simples com um único predicado de igualdade ou desigualdade usando histogramas estatísticos. Na seção intitulada, "Join Estimate Algorithm Changes", o artigo introduziu o conceito de "alinhamento grosseiro" usando limites mínimos e máximos de histograma:
Para junções com um único predicado de igualdade ou desigualdade, o CE legado une os histogramas nas colunas de junção alinhando os dois histogramas passo a passo usando interpolação linear. Esse método pode resultar em estimativas de cardinalidade inconsistentes. Portanto, o novo CE agora usa um algoritmo de estimativa de junção mais simples que alinha histogramas usando apenas limites mínimos e máximos de histograma.

Embora potencialmente menos consistente, o CE legado pode produzir estimativas de condição de junção simples ligeiramente melhores devido ao alinhamento passo a passo do histograma. O novo CE usa um alinhamento grosseiro. No entanto, a diferença nas estimativas pode ser pequena o suficiente para ter menos probabilidade de causar um problema de qualidade do plano.
Como um dos revisores técnicos do artigo, senti que um pouco mais de detalhes sobre essa mudança teria sido útil, mas isso não chegou à versão final. Este artigo adiciona alguns desses detalhes.

Exemplo de alinhamento de histograma grosseiro

O alinhamento grosseiro exemplo no White Paper usa a versão Data Warehouse do banco de dados de exemplo AdventureWorks. Apesar do nome, o banco de dados é bastante pequeno; o backup é de apenas 22,3 MB e se expande para cerca de 200 MB. Ele pode ser baixado por meio de links na página de documentação de instalação e configuração do AdventureWorks.

A consulta em que estamos interessados junta-se ao FactResellerSales e FactCurrencyRate mesas.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Esta é uma equijoin simples em uma única coluna portanto, qualifica-se para cardinalidade de junção e estimativa de seletividade usando alinhamento grosseiro de histograma.

Histogramas

Os histogramas que precisamos estão associados ao CurrencyKey coluna em cada tabela unida. Em uma nova cópia do banco de dados AdventureWorksDW, as estatísticas pré-existentes para o maior FactResellerSales tabela são baseados em uma amostra. Para maximizar a reprodutibilidade e tornar os cálculos detalhados o mais simples possível (evitando dimensionamento), a primeira coisa que faremos é atualizar as estatísticas usando uma varredura completa:

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

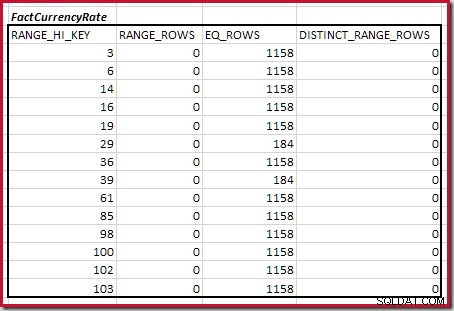
Essas tabelas têm o benefício amigável de demonstração de criar maxdiff pequenos e simples histogramas:

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;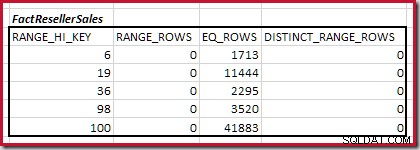

Combinando as etapas mínimas do histograma de correspondência

A primeira etapa do alinhamento grosseiro O cálculo é encontrar a contribuição para a cardinalidade de junção fornecida pela etapa mais baixa do histograma correspondente. Para nossos histogramas de exemplo, o valor mínimo da etapa correspondente está em RANGE_HI_KEY = 6 :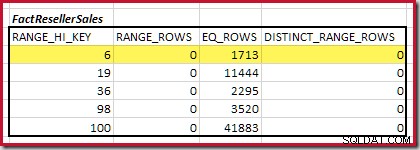

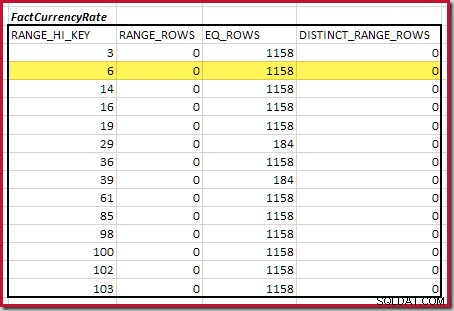
A cardinalidade de equijunção estimada apenas para esta etapa destacada é 1.713 * 1.158 =1.983.654 linhas .

Etapas correspondentes restantes

Em seguida, precisamos identificar o intervalo do histograma RANGE_HI_KEY aumenta ao máximo para possíveis correspondências de equijoin. Isso envolve avançar do mínimo encontrado anteriormente até que uma das entradas do histograma fique sem linhas. Os intervalos de equijoin correspondentes para o exemplo atual são destacados abaixo: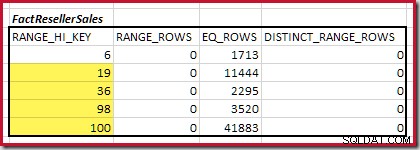

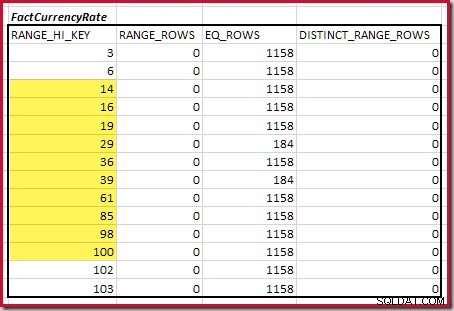
Esses dois intervalos representam as linhas restantes que podem contribuir para a cardinalidade da equijunção.

Estimativa Baseada em Frequência Grosseira

A questão agora é como realizar um grosseiro estimativa da cardinalidade equijoin dos passos destacados, usando as informações disponíveis.

O estimador de cardinalidade original teria realizado um alinhamento de histograma passo a passo de granulação fina usando interpolação linear, avaliado a contribuição de junção de cada etapa (assim como fizemos para o valor mínimo de etapa anterior) e somado cada contribuição de etapa para adquirir uma estimativa de junção completa. Embora esse procedimento faça muito sentido intuitivo, a experiência prática mostrou que essa abordagem refinada adicionava sobrecarga computacional e poderia produzir resultados de qualidade variável.

O estimador original tinha outra maneira de estimar a cardinalidade de junção quando as informações do histograma não estavam disponíveis ou eram avaliadas heuristicamente como inferiores. Isso é conhecido como estimativa baseada em frequência e usa as seguintes definições:

C – a cardinalidade (número de linhas)
D – o número de valores distintos
F – a frequência (número de linhas) para cada valor distinto
Observação C =D * F por definição

O efeito de uma equijunção das relações R1 e R2 em cada uma dessas propriedades é como mostrado abaixo:

F' =F1 * F2
D' =MIN(D1; D2) – supondo contenção
C' =D' * F' (novamente, por definição)

Estamos atrás de C', a cardinalidade da equijunção. Substituindo por D' e F' na fórmula e expandindo:

C' =D' * F'
C' =MIN(D1; D2) * F1 * F2
C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
agora, já que C1 =D1 * F1 e C2 =D2 * F2:
C' =MIN(C1 * F2, C2 * F1)
finalmente, já que F =C/D (também por definição):
C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

Observando que C1 * C2 é o produto das duas cardinalidades de entrada (junção cartesiana), fica claro que o mínimo dessas expressões será aquele com maior número de valores distintos:

C' =(C1 * C2) / MAX(D1; D2)

Caso tudo isso pareça um pouco abstrato, uma maneira intuitiva de pensar sobre a estimativa de equijunção baseada em frequência é considerar que cada valor distinto de uma relação se unirá a um número de linhas (a frequência média) na outra relação. Se tivermos 5 valores distintos de um lado e cada valor distinto do outro lado aparecer 3 vezes em média, uma estimativa de equijunção sensata (mas grosseira) é 5 * 3 =15.

Este não é um pincel tão amplo como pode parecer. Lembre-se de que os números de cardinalidade e valores distintos acima não vêm de toda a relação, mas apenas das etapas de correspondência acima do mínimo. Daí a estimativa grosseira entre os valores mínimo e máximo.

Cálculo de frequência

Podemos obter cada um desses parâmetros das etapas destacadas do histograma.

A cardinalidade C é a soma de EQ_ROWS e RANGE_ROWS .
O número de valores distintos D é a soma de DISTINCT_RANGE_ROWS mais um para cada etapa.

A cardinalidade C1 de correspondência de FactResellerSales passos é a soma das células destacadas: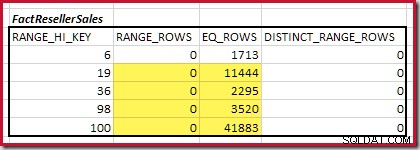

Isso dá C1 =59.142 linhas.

Não há linhas de intervalo distintas, portanto, os únicos valores distintos vêm dos próprios limites de quatro etapas, fornecendo D1 =4 .

Para a segunda tabela:

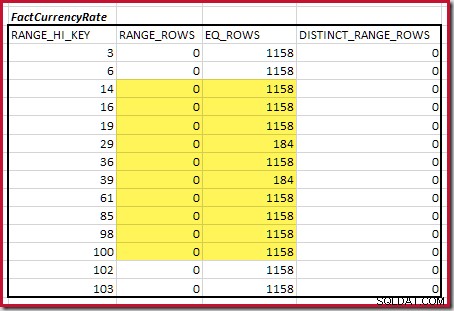
Isso dá C2 =9.632 . Novamente, não há linhas de intervalo distintas, portanto, os valores distintos vêm dos limites de dez etapas, D2 =10.

Concluindo a estimativa de equijoin

Agora temos todos os números que precisamos para a fórmula equijoin:

C' =(C1 * C2) / MAX(D1; D2)
C' =(59142 * 9632) / MAX(4; 10)
C' =569655744 / 10
C' =56.965.574,4

Lembre-se, esta é a contribuição das etapas do histograma acima do limite mínimo correspondido. Para concluir a estimativa de cardinalidade de junção, precisamos adicionar a contribuição dos valores mínimos da etapa de correspondência, que foi 1.713 * 1.158 =1.983.654 linhas.

A estimativa final de equijunção é, portanto, 56.965.574,4 + 1.983.654 =58.949.228,4 linhas ou 58.949.200 para seis algarismos significativos.

Este resultado é confirmado no plano de execução estimado para a consulta de origem:

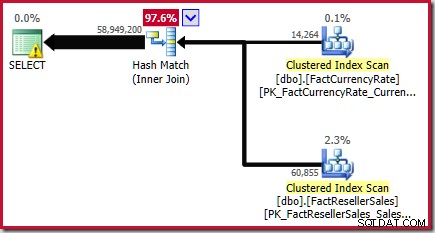
Conforme observado no Livro Branco, esta não é uma grande estimativa. O número real de linhas retornadas por esta consulta é 70.470.090 . A estimativa produzida pelo estimador de cardinalidade original ("legado") - usando o alinhamento de histograma passo a passo - é de 70.470.100 linhas.

Resultados melhores geralmente são possíveis com o método mais refinado, mas somente se as estatísticas forem uma representação muito boa da distribuição de dados subjacente. Não se trata simplesmente de manter as estatísticas atualizadas ou de usar a população de varredura completa. O algoritmo usado para empacotar informações em um máximo de 201 etapas de histograma não é perfeito e, em qualquer caso, muitas distribuições de dados do mundo real simplesmente não são capazes de tal fidelidade de histograma. Em média, as pessoas devem achar que o método mais grosseiro fornece estimativas perfeitamente adequadas e maior estabilidade com o novo CE.

Segundo Exemplo

Isso se baseia um pouco no exemplo anterior e não requer um download de banco de dados de exemplo.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

Os histogramas que mostram os passos mínimos correspondentes são:

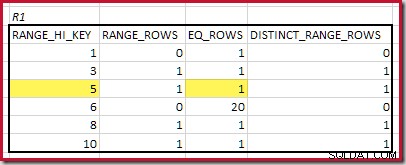
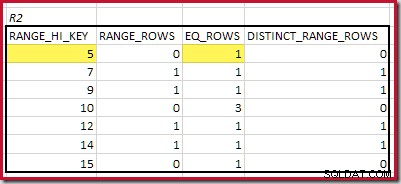
O RANGE_HI_KEY mais baixo que corresponde é 5. O valor de EQ_ROWS é 1 em ambos, então a cardinalidade de equijunção estimada é 1 * 1 =1 linha .

A correspondência mais alta RANGE_HI_KEY é 10. Destacando as linhas do histograma R1 para estimativa grosseira baseada em frequência: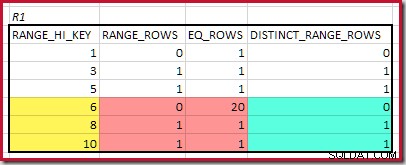

Somando EQ_ROWS e RANGE_ROWS dá C1 =24 . O número de linhas distintas é 2 DISTINCT_RANGE_ROWS (valores distintos entre etapas) mais 3 para os valores distintos associados a cada limite de etapa, resultando em D1 =5 .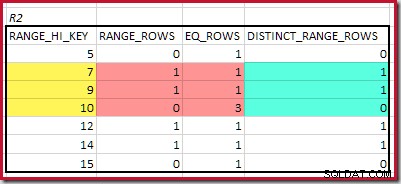

Para R2, somando EQ_ROWS e RANGE_ROWS dá C2 =7 . O número de linhas distintas é 2 DISTINCT_RANGE_ROWS (valores distintos entre etapas) mais 3 para os valores distintos associados a cada limite de etapa, resultando em D2 =5 .

A estimativa de equijunção C' é:

C' =(C1 * C2) / MAX(D1; D2)
C' =(24 * 7) / 5
C' =33,6

Adicionando a 1 linha da correspondência mínima de etapas fornece uma estimativa total de 34,6 linhas para a equijunção:

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

O plano de execução estimado mostra uma estimativa que corresponde ao nosso cálculo:

Isso não está exatamente certo, mas o estimador de cardinalidade "legado" não funciona melhor, estimando 15,25 linhas versus 27 reais:

Para um tratamento completo, também teríamos que adicionar uma contribuição final das etapas nulas do histograma correspondentes, mas isso é incomum para equijunções (que normalmente são escritas para rejeitar nulos) e uma extensão relativamente direta para o leitor interessado.

Considerações finais

Espero que os detalhes do artigo preencham algumas lacunas para quem já se perguntou sobre "alinhamento grosseiro". Observe que este é apenas um pequeno componente no estimador de cardinalidade. Existem vários outros conceitos e algoritmos importantes usados para estimativa de junção, principalmente a maneira como os predicados sem junção são avaliados e como as junções mais complexas são tratadas. Muitas das partes realmente importantes são muito bem abordadas no Livro Branco.