Tabela com coordenadas de uma grade hexagonal que cobre o mundo

Algum tempo atrás eu adaptei uma function para gerar hexágonos que podem ser exatamente o que você está procurando. Ele pega os parâmetros de largura da célula e as coordenadas dos cantos sudoeste e nordeste e gera uma grade hexagonal.

CREATE OR REPLACE FUNCTION create_hexagons(width FLOAT, xmin FLOAT, ymin FLOAT, xmax FLOAT, ymax FLOAT)
RETURNS TABLE (_gid INTEGER, _geom GEOMETRY) AS $$
DECLARE
  b FLOAT := width/2;
  a FLOAT := b/2;
  c FLOAT := 2*a;
  height FLOAT := 2*a+c;
  ncol FLOAT := ceil(abs(xmax-xmin)/width);
  nrow FLOAT := ceil(abs(ymax-ymin)/height);
  polygon_string VARCHAR := 'POLYGON((' || 
    0 || ' ' || 0 || ' , ' || b || ' ' || a || ' , ' || b || ' ' || a+c || ' , ' || 0 || ' ' || a+c+a || ' , ' ||
   -1*b || ' ' || a+c || ' , ' || -1*b || ' ' || a || ' , ' || 0 || ' ' || 0 || '))';
BEGIN
  CREATE TEMPORARY TABLE tmp (gid serial NOT NULL PRIMARY KEY,geom GEOMETRY(POLYGON)) ON COMMIT DROP;
  INSERT INTO tmp (geom)   
  SELECT ST_Translate(geom, x_series*(2*a+c)+xmin, y_series*(2*(c+a))+ymin)
  FROM generate_series(0, ncol::INT, 1) AS x_series,
       generate_series(0, nrow::INT,1 ) AS y_series,
    (SELECT polygon_string::GEOMETRY AS geom
     UNION
     SELECT ST_Translate(polygon_string::GEOMETRY, b, a + c) AS geom) AS two_hex;
    ALTER TABLE tmp ALTER COLUMN geom TYPE GEOMETRY(POLYGON, 4326) USING ST_SetSRID(geom, 4326);   
    RETURN QUERY (SELECT gid, geom FROM tmp);    
END;
$$ LANGUAGE plpgsql;

Esta função retorna uma tabela com as colunas _gid e _geom , contendo um identificador e a geometria para cada hexágono, respectivamente.

CREATE TABLE t AS
SELECT * FROM create_hexagons(1.0, -180, -90, 180, 45)

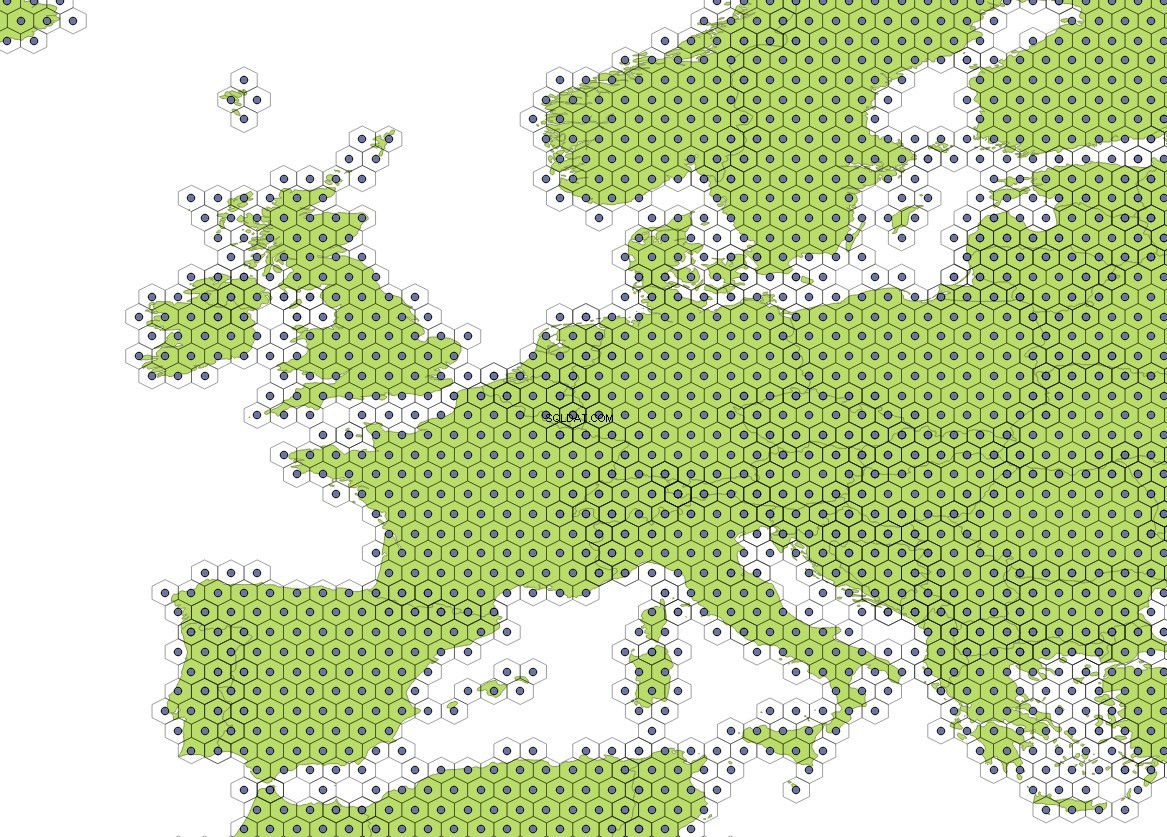
Com esses parâmetros, a função gera uma grade com 98192 hexágonos cobrindo o mundo inteiro:

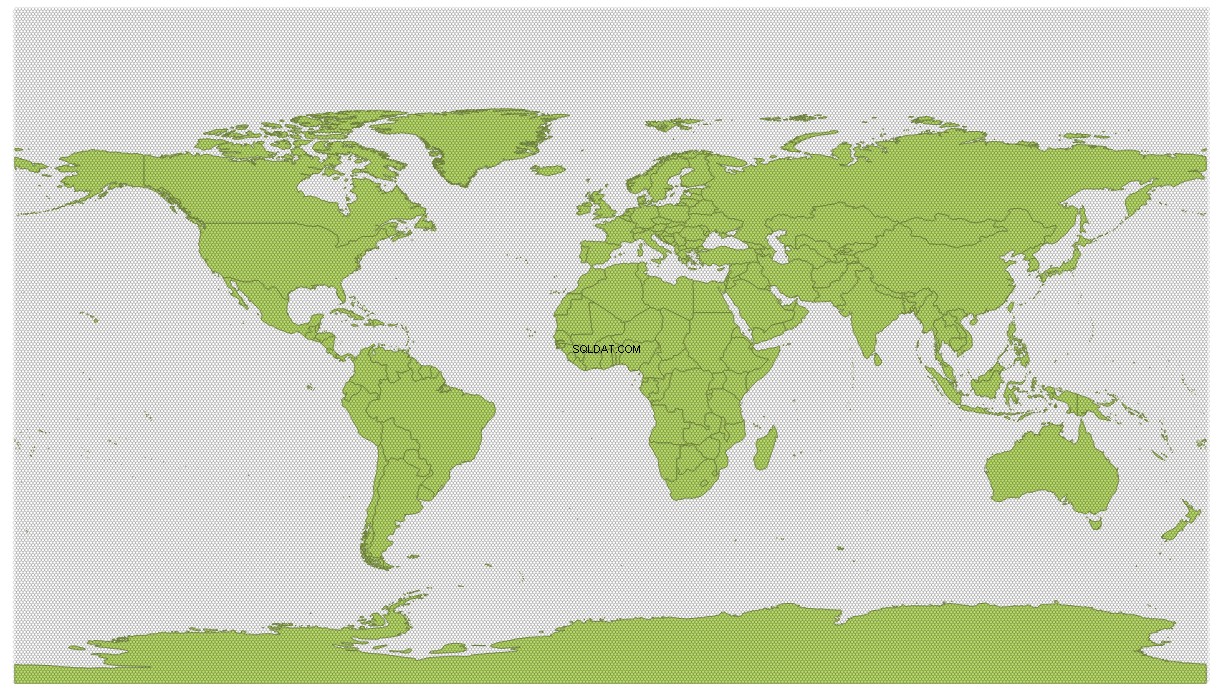
Aqui um pouco mais perto, para que você possa ver a grade:

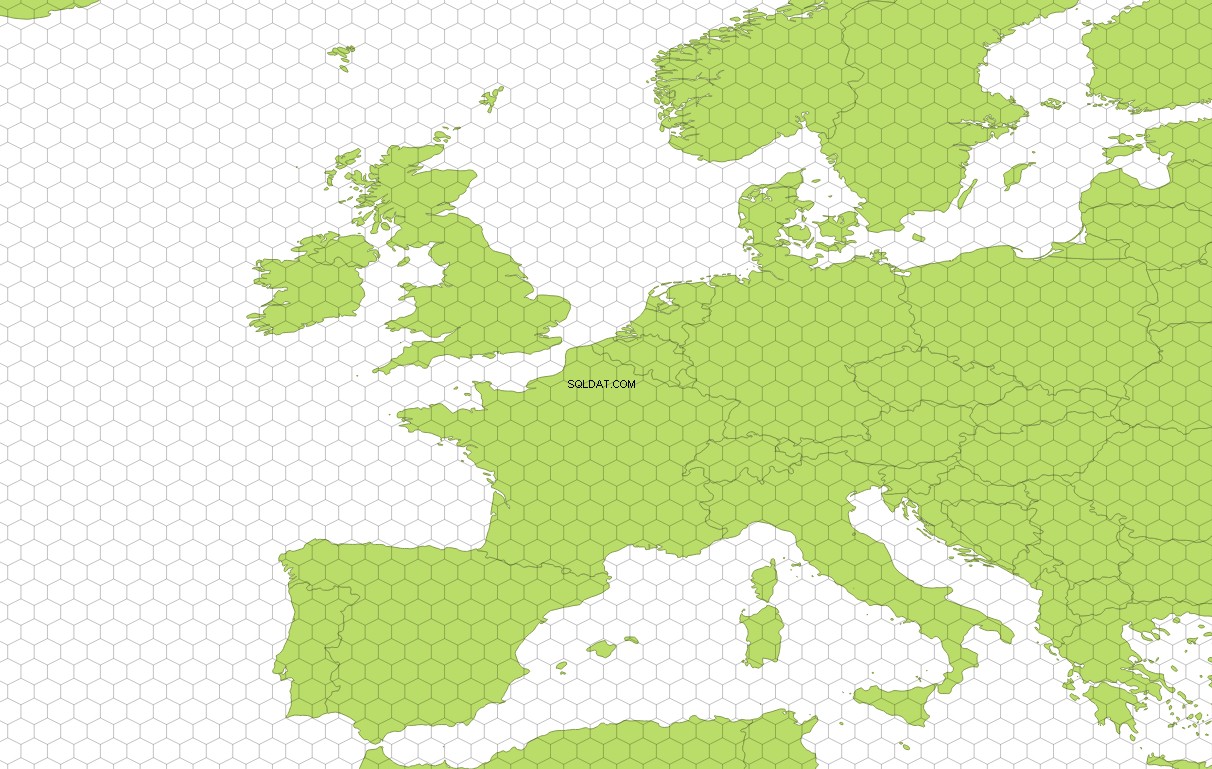
Se estiver interessado apenas em cobrir a terra, você pode criar um subconjunto desses hexágonos com base em uma geometria de sua escolha usando ST_Intersects :

CREATE TABLE t_overlap AS 
SELECT t._gid,t._geom FROM t,world 
WHERE ST_Intersects(world.geom,t._geom)

Esta consulta criará um subconjunto com uma grade contendo 35911 hexágonos, que se cruzam com as geometrias do mapa do mundo:

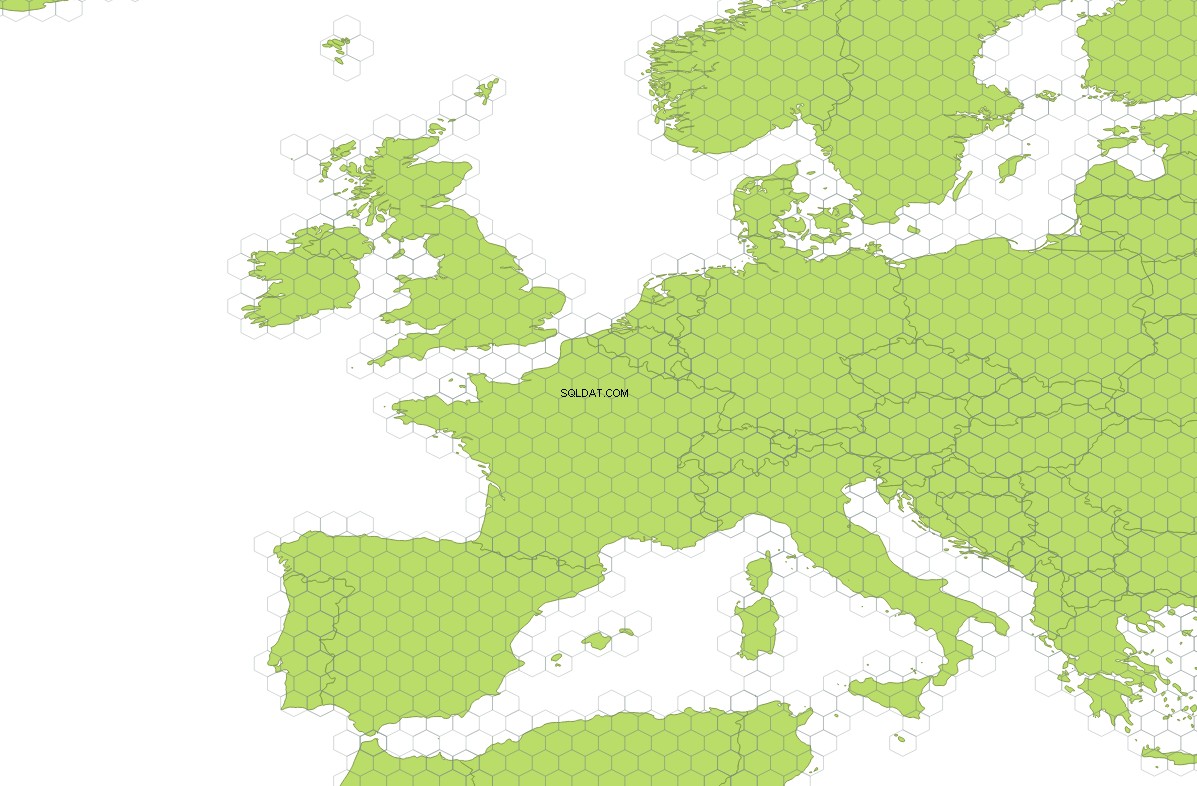
O mapa do mundo usado nesta resposta pode ser baixado como shapefile here .

Produto final:- Uma tabela contendo o ponto central de cada hexágono em uma grade hexagonal que cobre todo o mundo. - Os hexágonos têm uma área fixa

Gerar os centroides para cada hexágono também não é grande coisa (veja ST_Centroid ):

CREATE TABLE t_overlap_centroid AS
SELECT ST_Centroid(_geom) FROM t_overlap;